Câu hỏi
a) Một khu vườn hình chữ nhật có kích thước là 25m và 40m. Người ta tăng mỗi kích thước của khu vườn thêm x (mét). Gọi S và P theo thứ tự là diện tích và chu vi của khu vườn mới tính theo x. Hỏi các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao? Tính giá trị của x khi biết giá trị tương ứng của P là 144 (tính theo đơn vị mét).
b) Cho hàm số y = -2x + 3 có đồ thị là (d1) và hàm số y = x có đồ thị là (d2). Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy. Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính.
- A a) x= 2,5 ; b) tọa độ giao điểm là (2;1)
- B a) x= 3,5 ; b) tọa độ giao điểm là (1;1)
- C a) x= 3 ; b) tọa độ giao điểm là (1;0)
- D a) x= 4 ; b) tọa độ giao điểm là (1;2)
Lời giải chi tiết:
a)
Chiều rộng của khu vườn sau khi tăng thêm x(m) là: \(25 + x\) (mét)
Chiều dài của khu vườn sau khi tăng thêm x(m) là: \(40 + x\) (mét)
Chu vi của khu vườn mới là: \(P = \left( {25 + x + 40 + x} \right).2 = \left( {65 + 2x} \right).2 = 4x + {130^{}}\left( m \right)\)
Diện tích của khu vườn mới là: \(S = \left( {25 + x} \right).\left( {40 + x} \right) = {x^2} + 65x + {1000^{}}\left( {{m^2}} \right)\)
Do: \(P = 4x + 130\) có dạng \(y = ax + b\) với \(a = 4 \ne 0\), \(b = 130\) nên \(P = 4x + 130\) là hàm số bậc nhất.
Do: \(S = {x^2} + 65x + 1000\) không có dạng \(y = ax + b\) nên không phải là hàm số bậc nhất.
v Với P = 144 (m), thay vào \(P = 4x + 130\), ta được: \(144 = 4x + 130 \Leftrightarrow 4x = 14 \Leftrightarrow x = 3,5\left( m \right)\)
b)
Bảng giá trị:

Đồ thị:
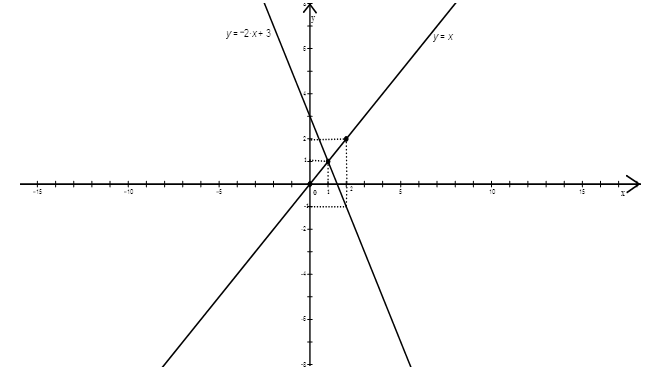
Phương trình hoành độ giao điểm của (d1) và (d2): \( - 2x + 3 = x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1\)
Thay x = 1 vào (d2) \( \Rightarrow y = 1\)
Vậy: Tọa độ giao điểm của (d1) và (d2) là \(\left( {1{;^{}}1} \right)\).







