Câu hỏi
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\ln \left( {{x}^{2}}+1 \right)-m\left( x+2 \right)\) đồng biến trên khoảng \(\left( -\infty ;+\infty \right)\)
- A \(\left( -\infty ;-1 \right)\)
- B \(\left[ 1;+\infty \right)\)
- C \(\left( -\infty ;-1 \right]\)
- D \(\left[ -1;1 \right]\)
Phương pháp giải:
+) Hàm số đồng biến trên R khi và chỉ khi \(y'\ge 0\,\,\forall x\in R\) và chỉ bằng 0 tại hữu hạn điểm.
+) Cô lập m, đưa về bất phương trình dạng \(m\le f\left( x \right)\,\,\forall x\in R\Leftrightarrow m\le \underset{R}{\mathop{\min }}\,f\left( x \right)\)
Lời giải chi tiết:
Hàm số đồng biến trên R khi và chỉ khi \(y'=\frac{2x}{{{x}^{2}}+1}-m\ge 0\,\,\forall x\in R\) và chỉ bằng 0 tại hữu hạn điểm.
\(\Leftrightarrow m\le \frac{2x}{{{x}^{2}}+1}=f\left( x \right)\,\,\forall x\in R\Rightarrow m\le \underset{R}{\mathop{\min }}\,f\left( x \right)\)
Ta có \(f'\left( x \right)=\frac{2\left( {{x}^{2}}+1 \right)-2x.2x}{{{\left( x+1 \right)}^{2}}}=\frac{-2{{x}^{2}}+2}{{{\left( x+1 \right)}^{2}}}=0\Leftrightarrow x=\pm 1\)
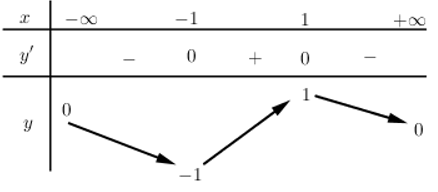
BBT:
\(\Rightarrow \underset{R}{\mathop{\min }}\,f\left( x \right)=-1\Leftrightarrow m\le -1\)
Khi m = -1 ta có \(y'=\frac{2x}{{{x}^{2}}+1}+1=\frac{{{\left( x+1 \right)}^{2}}}{{{x}^{2}}+1}=0\Leftrightarrow x=-1\Rightarrow y'=0\) tại hữu hạn điểm. Do đó m = -1 thỏa mãn.
Chọn C.