Câu hỏi
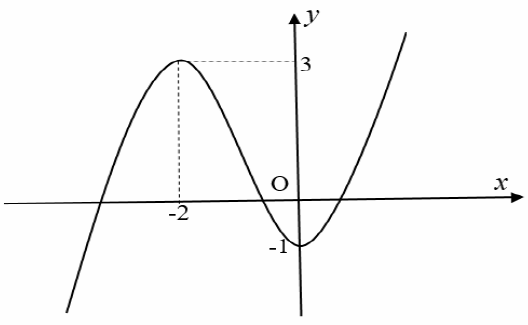
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tìm tập hợp tất cả các giá trị của \(m\) để đồ thị hàm số \(y = f\left( {\left| x \right| + m} \right)\) có \(5\) điểm cực trị.
- A \(m < 2.\)
- B \(m > 2.\)
- C \(m > - 2.\)
- D \(m < - 2.\)
Phương pháp giải:
Ta thấy đồ thị hàm số \(y = f\left( {x + m} \right)\) là đồ thị hàm số \(y = f\left( x \right)\) tịnh tiến sang bên trái một đoạn bằng \(m\) khi \(m > 0,\) tịnh tiến sang bên phải một đoạn bằng \(\left| m \right|\) khi \(m < 0.\)
Hơn nữa đồ thị hàm số \(y = f\left( {\left| x \right| + m} \right)\) là đồ thị hàm số \(y = f\left( {x + m} \right)\) lấy trong khoảng \(x > 0\) và phần đồ thị hàm số này lấy đối xứng qua trục \(Oy.\)
Vì vậy để hàm số có 5 cực trị thì đồ thị phải tịnh tiến về bên phải sao cho điểm hai điểm cực trị phải nằm hoàn toàn bên phải của trục tung.
Lời giải chi tiết:
Ta thấy đồ thị hàm số \(y = f\left( {x + m} \right)\) là đồ thị hàm số \(y = f\left( x \right)\) tịnh tiến sang bên trái một đoạn bằng \(m\) khi \(m > 0,\) tịnh tiến sang bên phải một đoạn bằng \(\left| m \right|\) khi \(m < 0.\)
Hơn nữa đồ thị hàm số \(y = f\left( {\left| x \right| + m} \right)\) là đồ thị hàm số \(y = f\left( {x + m} \right)\) lấy trong khoảng \(x > 0\) và phần đồ thị hàm số này lấy đối xứng qua trục \(Oy.\)
Vì vậy để hàm số có 5 cực trị thì đồ thị phải tịnh tiến về bên phải sao cho điểm hai điểm cực trị phải nằm hoàn toàn bên phải của trục tung. Hay đồ thị hàm số đã cho phải tịnh tiến một đoạn lớn hơn 2
\( \Leftrightarrow \left\{ \begin{array}{l}m < 0\\\left| m \right| > 2\end{array} \right. \Leftrightarrow m < - 2.\)
Chọn D.







