Môn Lý - Lớp 12
40 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng
Câu hỏi
Hai chất điểm dao động điều hòa trên cùng một trục Ox, coi trong quá trình dao động hai chất điểm không va chạm vào nhau. Biết phương trình dao động của hai chất điểm lần lượt là \({x_1} = 10c{\rm{os}}\left( {{\rm{4}}\pi {\rm{t + }}{\pi \over {\rm{3}}}} \right)\,cm\) và \({x_2} = 10\sqrt 2 c{\rm{os}}\left( {{\rm{4}}\pi {\rm{t + }}{\pi \over {{\rm{12}}}}} \right)\,cm\). Hai chất điểm cách nhau 5cm ở thời điểm lần thứ 2017 kể từ lúc t = 0 lần lượt là:
- A 1008 s.
- B \({{6041} \over 8}s\)
- C \({{2017} \over 8}s\)
- D \({{2017} \over {12}}s\)
Lời giải chi tiết:
Đáp án C
+ Dễ dàng tính được: \(d = \left| {{x_1} - {x_2}} \right| = 10\cos \left( {4\pi t + {{5\pi } \over 6}} \right)\). Bài toán khoảng cách quy về bài toán1 vật dao động qua vị trí cách vị trí cân bằng 5 cm. Tới đây ta giải bình thường
+ Trong 1chu kì hai chất điểm cách nhau 5cm sẽ có 4 vị trí phù hợp trên đường tròn của d.
Tách:
\(\left\{ \matrix{ n = 2017 = 504.4 + 1 \hfill \cr t = 504.T + {t_0} \hfill \cr} \right.\)
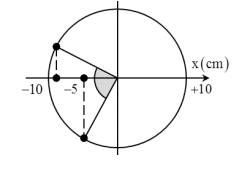
Tại t = 0 \( = > \Phi = {{5\pi } \over 6}\).
Từ đường tròn xác định được: \(\Delta {\varphi _0} = {\pi \over 2} = > {t_0} = {T \over 4}\)
Câu hỏi trước
