Câu hỏi
Một sóng cơ lan truyền trong môi trường liên tục từ điểm M đến điểm N cách M một đoạn 7λ/3(cm) (λ là bước sóng). Sóng truyền với biên độ A không đổi. Biết phương trình sóng tại M có dạng uM=3cos2πt (uM tính bằng cm, t tính bằng giây. Vào thời điểm t1 tốc độ dao động của phần tử M là 6π(cm/s) thì tốc độ dao động của phần tử N là
- A 3π (cm/s).
- B 4π (cm/s).
- C
6π (cm/s).
- D 0,5π (cm/s).
Phương pháp giải:
Sử dụng vòng tròn lượng giác, công thức tính độ lệch pha \(\Delta \varphi = {{2\pi d} \over \lambda }\)
Lời giải chi tiết:
- Độ lệch pha giữa M và N là \(\Delta \varphi = {{2\pi d} \over \lambda } = {{2\pi .{{7\lambda } \over 3}} \over \lambda } = 2\pi + {{2\pi } \over 3}(rad)\)
Do sóng truyền từ M đến N nên M dao động sớm pha 2π/3 so với N
- Tại thời điểm t1, tốc độ dao động của phần tử tại M là 6π cm/s = vMmax => M đang ở VTCB
Ta biểu diễn vị trí hai điểm M và N trên vòng tròn lượng giác
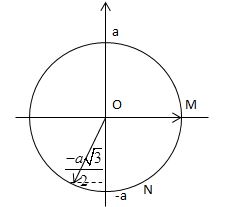
Từ hình vẽ ta xác định được li độ của điểm N tại thời điểm t1 là \({u_N} = - {{a\sqrt 3 } \over 2} = - 1,5\sqrt 3 cm\)
Tốc độ dao động của điểm N khi đó là \({v_N} = \omega \sqrt {A_N^2 - u_N^2} = 2\pi \sqrt {{3^2} - {2^2}.3} = 3\pi cm/s\)
Chọn A







