Câu hỏi
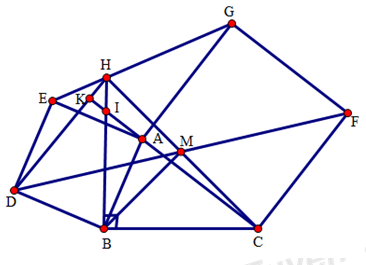
Cho tam giác ABC \(\left( \widehat{A\,\,}<{{90}^{0}} \right)\). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trung điểm của đoạn thẳng DF. Chứng minh rằng tam giác MBC cân tại M.
Phương pháp giải:
+ Vẽ thêm điểm H sao cho tam giác BHC vuông cân đỉnh B, H thuộc nửa mặt phẳng bờ BC có chứa điểm A.
+ Chứng minh M là trung điểm của HC để suy ra MB = MC.
+ Chứng minh MB vuông góc với MC để suy ra điều phải chứng minh.
Lời giải chi tiết:
Trên nửa mặt phẳng bờ BC có chưa A dựng tam giác BHC vuông cân đỉnh B.
Xét tam giác BHD và tam giác BCA có:
DB = BA (Vì ADBE là hình vuông)
\(\widehat{DBH}=\widehat{ABC}\) (vì cùng phụ với góc HBA)
BH = BC (vì tam giác BHC vuông cân đỉnh B)
Do đó: \(\Delta BHD=\Delta BCA\,\,(c.g.c)\), suy ra \(DH=AC,\widehat{BHD}=\widehat{BCA}\).
AC cắt HD tạ K, cắt BH tại I.
Xét tam giác IHK và tam giác ICB có: \(\widehat{HIK}=\widehat{CIB}\) (đối đỉnh), \(\widehat{BHD}=\widehat{BCA}\), do đó \(\widehat{HKI}=\widehat{IBC}={{90}^{0}}\Rightarrow KC\bot DH\)
Mặt khác \(KC\bot CF\), do đó DH // CF.
Ta có DH = CF (= AC) và DH // CF nên DHFC là hình bình hành.
Mà M là trung điểm của DF nên M là trung điểm của HC, suy ra tam giác MBC vuông cân đỉnh M.