Câu hỏi
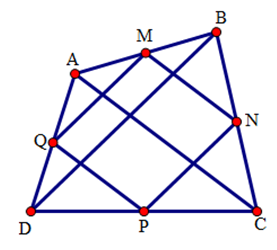
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì để M, N, P, Q là bốn đỉnh của:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?
Phương pháp giải:
Dựa vào dấu hiệu nhận biết các hình:
+) Hình chữ nhật, hình thoi, hình vuông để tìm ra điều kiện của hai đường chéo AC và BD tương ứng.
Lời giải chi tiết:
Xét tam giác ABD có:
M là trung điểm của AB (gt)
Q là trung điểm của AD (gt)
\(\Rightarrow \) QM là đường trung bình của tam giác ABD. (định lý)
Do đó QM // BD và \(QM=\frac{1}{2}BD\) (1)
CM tương tự ta cũng có NP là đường trung bình của tam giác BCD.
\(\Rightarrow \left\{ \begin{align} & NP//BD \\ & NP=\frac{1}{2}BD\,\,\,\,\left( 2 \right) \\ \end{align} \right.\)
Từ (1) và (2) ta suy ra MNPQ là hình bình hành (dấu hiệu nhận biết).
a) Để MNPQ là hình chữ nhật \(\Leftrightarrow MN\bot NP\Leftrightarrow AC\bot BD\) (vì MN // AC, NP // BD)
Điều kiện cần tìm là hai đường chéo BD và AC vuông góc với nhau.
b) Để MNPQ là hình thoi \(\Leftrightarrow MN=NP\Leftrightarrow AC=BD\) (vì \(MN=\frac{1}{2}AC,NP=\frac{1}{2}BD\))
Điều kiện cần tìm là hai đường chéo BD và AC bằng nhau.
c) Để MNPQ là hình vuông
\( \Leftrightarrow \left\{ \begin{array}{l}MN \bot PQ\\MN = PQ\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC \bot BD\\AC = BD\end{array} \right.\)
Điều kiện cần tìm là hai đường chéo BD và AC bằng nhau và vuông góc với nhau.