Môn Lý - Lớp 12
40 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng
Câu hỏi
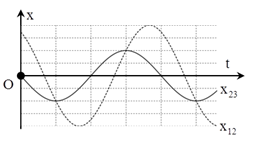
Cho ba dao động điều hòa cùng phương cùng tần số, có phương trình lần lượt là \({x_1} = 2a\cos \left( {\omega t} \right) cm\), \({x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)cm\), \({x_3} = a\cos \left( {\omega t + \pi } \right) cm\). Gọi \({x_{12}} = {x_1} + {x_2}\) ;\({x_{23}} = {x_2} + {x_3}\). Biết đồ thị sự phụ thuộc của x12 và x23 vào thời gian như hình vẽ. Giá trị của φ2 là:
- A \({\pi \over 3}\)
- B \({\pi \over 4}\)
- C \({2\pi \over 3}\)
- D \({\pi \over 6}\)
Lời giải chi tiết:
Đáp án C
+ Từ đồ thị ta thấy rằng \({A_{12}} = 2{A_{23}}\)
Do đó: \({\left( {2a} \right)^2} + A_2^2 + 2\left( {2a} \right){A_2}\cos \left( {{\varphi _2}} \right) = 4\left[ {{{\left( a \right)}^2} + A_2^2 + 2a{A_2}\cos \left( {{\varphi _2} - \pi } \right)} \right]\).
Ta chú ý rằng \(\cos \left( {{\varphi _2} - \pi } \right) = - \cos \left( {{\varphi _2}} \right)\)
Biến đổi toán học ta tìm được \(\cos \left( {{\varphi _2}} \right) = - 0,5 \Rightarrow {\varphi _2} = {{2\pi } \over 3}\) rad.
Câu hỏi trước
