Câu hỏi
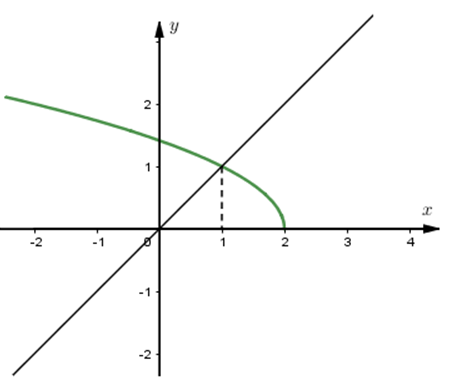
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đồ thị hàm số \(y=\sqrt{2-x},\) \(y=x,\,\,\,y=0\) xung quanh trục \(Ox\) được tính theo công thức nào sau đây ?
- A \(V=\pi \int\limits_{0}^{1}{\left( 2-x \right)\text{d}x}+\pi \int\limits_{1}^{2}{{{x}^{2}}\,\text{d}x}.\)
- B \(V=\pi \int\limits_{0}^{1}{\left( 2-x \right)\text{d}x}.\)
- C \(V=\pi \int\limits_{0}^{1}{x\,\text{d}x}+\pi \int\limits_{1}^{2}{\sqrt{2-x}\,\text{d}x}.\)
- D \(V=\pi \int\limits_{0}^{1}{{{x}^{2}}\,\text{d}x}+\pi \int\limits_{1}^{2}{\left( 2-x \right)\,\text{d}x}.\)
Phương pháp giải:
Tìm đầy đủ các giao điểm, chia tích phân cần tính thành các tích phân thích hợp.
Lời giải chi tiết:
Xét các phương trình hoành độ giao điểm : \(\sqrt{2-x}=x\Leftrightarrow \left\{ \begin{align} & 0\le x\le 2 \\ & 2-x={{x}^{2}} \\\end{align} \right.\Leftrightarrow x=1;\,\,\sqrt{2-x}=0\Leftrightarrow x=2\)
Thể tích vật tròn xoay cần tìm là thể tích khối tròn xoay thu được khi quay hai hình phẳng \(\left( {{H}_{1}} \right):\left\{ y=x;\,\,x=0;\,\,x=1 \right\}\) và \(\left( {{H}_{2}} \right):\left\{ y=\sqrt{2-x};\,\,x=1;\,\,x=2 \right\}.\)
Vậy thể tích khối tròn xoay là \(V=\pi \int\limits_{0}^{1}{{{x}^{2}}\,\text{d}x}+\pi \int\limits_{1}^{2}{\left( 2-x \right)\,\text{d}x}.\)
Chọn D.