Câu hỏi
Hàm số \(y=\frac{{{x}^{4}}}{4}-2{{x}^{2}}+3\) nghịch biến trên khoảng nào?
- A \(\left( -\infty ;-2 \right)\) và \(\left( 0;2 \right)\)
- B \(\left( -2;0 \right)\)
- C \(\left( 2;+\infty \right)\)
- D \(\left( -2;0 \right)\) và \(\left( 2;+\infty \right)\)
Phương pháp giải:
- Tính \(y’\) và tìm các khoảng làm cho \(y'<0\).
Lời giải chi tiết:
Ta có: \(y'={{x}^{3}}-4x\)
\(y' = 0 \Rightarrow {x^3} - 4x = 0 \Leftrightarrow x\left( {x - 2} \right)\left( {x + 2} \right) = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = - 2\\x = 2\end{array} \right.\)
Xét dấu :
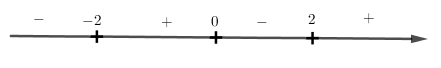
Từ bảng xét dấu ta dễ dàng quan sát được hàm số nghịch biến trên các khoảng \(\left( -\infty ,-2 \right)\) và \(\left( 0,2 \right)\).
\(\Rightarrow \)
Đáp án A
Câu hỏi trước
