Phương pháp giải:

Công thức tính thể tích khối nón: \(V=\frac{1}{3}S.h\) với \(S\) là diện tích hình tròn đáy và \(h\) là đường cao.

Lời giải chi tiết:

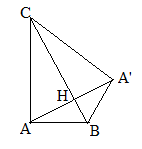
Gọi \(A'\) đối xứng với \(A\) qua \(BC\). Khi quay tam giác quanh trục \(BC\) ta sẽ được hai khối nón có đáy là hình tròn tâm \(H\) bán kính \(AH\) và lần lượt có chiều cao là \(BH\) và \(CH\).

Ta có:

\(\begin{array}{l}AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3 \\ \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{a.a\sqrt 3 }}{{2a}} = \frac{{a\sqrt 3 }}{2}\end{array}\)

\(\Rightarrow V=\frac{1}{3}\pi A{{H}^{2}}.BH+\frac{1}{3}\pi A{{H}^{2}}.CH=\frac{1}{3}.\pi .A{{H}^{2}}.BC=\frac{1}{3}\pi {{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}.2a=\frac{\pi {{a}^{3}}}{2}.\)

Đáp án A.