Phương pháp giải:

- Tính thể tích khối nón có được khi quay tam giác \(ACH\) quanh \(AB\) (hay \(AH\)) bằng công thức \(V=\frac{1}{3}{{S}_{d}}.h\) với đáy là hình tròn tâm \(H\) bán kính \(CH\) và chiều cao là \(AH\).

- Tìm GTLN của thể tích dựa vào phương pháp xét hàm, từ đó tìm được \(AH\).

Lời giải chi tiết:

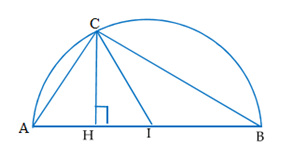
Thể tích khối nón khi quay \(\Delta ACH\) quay quanh AB:

\(V=\frac{1}{3}AH.\pi .C{{H}^{2}}=\frac{1}{3}AH.\pi \left( AH.AB-A{{H}^{2}} \right)=\frac{2R\pi }{3}.A{{H}^{2}}-\frac{\pi }{3}A{{H}^{3}}\)

Xét hàm số: \(y=\frac{2\pi R}{3}{{t}^{2}}-\frac{\pi }{3}{{t}^{3}}\) với t = AH.

\(\Rightarrow y'=\frac{4\pi R}{3}t-\pi {{t}^{2}}\)

\(y = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\left( L \right)\\t = \frac{{4R}}{3} \to AH = \frac{{4R}}{3}.\end{array} \right.\)

\(\Rightarrow HB=AB-AH=\frac{2R}{3}\Rightarrow CH=\frac{2R\sqrt{2}}{3}\)

\(\Rightarrow \tan \widehat{CAB}=\frac{CH}{AH}=\frac{1}{\sqrt{2}}\Rightarrow \widehat{CAB}=\arctan \frac{1}{\sqrt{2}}.\)

Đáp án C