Câu hỏi
Cho hàm số \(y=f(x)\) xác định và có đạo hàm \(f'\left( x \right)\). Đồ thị của hàm số \(f'\left( x \right)\)như hình dưới đây. Khẳng định nào sau đây là đúng?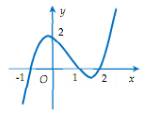
- A Hàm số \(y=f(x)\) có ba điểm cực trị.
- B Hàm số \(y=f(x)\) đồng biến trên khoảng \(\left( -\infty ;2 \right).\)
- C Hàm số \(y=f(x)\)nghịch biến trên khoảng \(\left( 0;1 \right)\).
- D Hàm số \(y=f(x)\)đồng biến trên khoảng \(\left( -\infty ;-1 \right)\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y=f'\left( x \right)\) để tìm khoảng dương, âm của \(f'\left( x \right)\), từ đó tìm được khoảng đồng biến, nghịch biến của \(f\left( x \right)\).
Lời giải chi tiết:
Từ đồ thị hàm số \(y=f'\left( x \right)\) suy ra hàm số \(y=f(x)\) nghịch biến trên \(\left( -\infty ;-1 \right)\) và \(\left( 1;2 \right)\) (làm \(y'\) âm) và đồng biến trên \(\left( -1;1 \right)\) (làm \(y'\) dương).
Suy ra B, C, D sai và A đúng.
Đáp án A.
Câu hỏi trước
