Phương pháp giải:

Vận dụng bài toán con lắc chịu tác dụng của lực điện.

Lời giải chi tiết:

Đáp án D

$$P = mg,{\rm{ }}{F_d} = qE$$

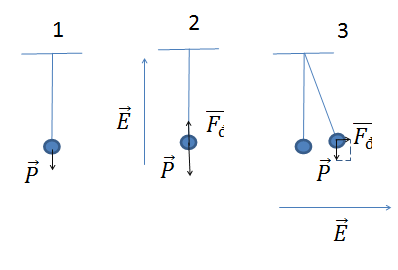
Biểu diễn lực như hình, ta có: 

Khi chưa có điện trường:  ${T_1} = 2\pi \sqrt {{l \over g}} $ 

Khi điện trường có phương thẳng đứng: $${T_2} = 2\pi \sqrt {{l \over {g'}}} $$

  trong đó: $$g' = \left| {g - {{qE} \over m}} \right|$$ 

Khi điện trường có phương ngang: $${T_3} = 2\pi \sqrt {{l \over {g}}} $$

 trong đó: $$g = \sqrt {{g^2} + {{({{qE} \over m})}^2}} $$

Ta có:   $${{{T_1}} \over {{T_2}}} = \sqrt {{{g'} \over g}}  \to {{\left| {g - {{qE} \over m}} \right|} \over g} = {({{{T_1}} \over {{T_2}}})^2} = {1 \over 4} \to 4(g - {{qE} \over m}) = g \to {{qE} \over m} = {3 \over 4}g$$

 $${{{T_1}} \over {{T_3}}} = \sqrt {{{g} \over g}}  \to \sqrt {{{\sqrt {{g^2} + {{({{qE} \over m})}^2}} } \over g}}  = \sqrt {{5 \over 4}}  \to {T_3} = {T_1}{2 \over {\sqrt 5 }} = 1,79{\rm{s}}$$