Phương pháp giải:

Sử dụng kiến thức:

-          Vẽ đồ thị hàm số với các miền tương ứng

-          Biện luận phương trình dựa vào đồ thị hàm số.

Lời giải chi tiết:

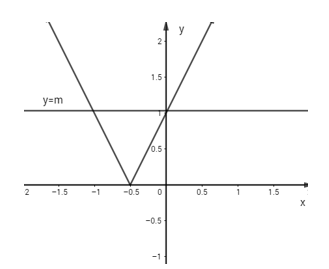
Đặt \(y = |2x + 1|\)

Ta có: \(y = |2x + 1| = \left\{ \begin{array}{l}2x + 1\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{khi}&{x \ge \frac{{ - 1}}{2}}\end{array}}\end{array}\\ - 2x - 1\begin{array}{*{20}{c}}{}&{khi\begin{array}{*{20}{c}}{}&{x < \frac{{ - 1}}{2}}\end{array}}\end{array}\end{array} \right.\)

Phương trình \(|2x + 1| = m\) vô nghiệm

 \( \Leftrightarrow \)đường thẳng y = m không cắt đồ thị hàm số \(y = |2x + 1| \Leftrightarrow m < 0.\)

Chọn C.