Phương pháp giải:

Nếu tồn tại đạo hàm của hàm số\(y = f\left( x \right)\) tại \(x = {x_0}\) mà \(f'\left( {{x_0}} \right) = 0\) và \(f'\left( x \right)\) đổi dấu qua \({x_0}\) thì \(x = {x_0}\) là một điểm cực trị của hàm số \(y = f\left( x \right)\).

Lời giải chi tiết:

Xét phương trình 

\(f'\left( x \right) = 0 \Leftrightarrow {\left( {x + 1} \right)^2}{\left( {x - 2} \right)^3}\left( {2x + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\\x = - \frac{3}{2}\end{array} \right.\)

Xét dấu \(f'\left( x \right)\) ta có:

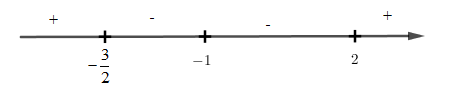
Từ đó ta thấy \(f'\left( x \right)\) chỉ đổi dấu qua hai nghiệm \({x_1} =  - \frac{3}{2};{x_2} = 2\) nên hàm số \(y = f\left( x \right)\) có hai điểm cực trị.

Chọn A.