Phương pháp giải:

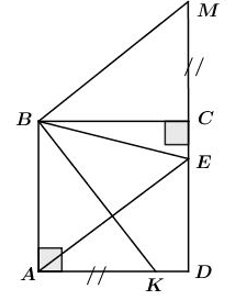
Phương pháp: Vẽ thêm điểm M trên tia đối của tia CD sao cho \(CM=AK\) . Từ đó \(AK+CE=CM+CE=EM\) . Bài toán đưa về việc chứng minh \(EM=BE\)

Lời giải chi tiết:

Cách giải:

Trên tia đối của tia CD lấy điểm M  sao cho \(CM=AK\) . Ta có: \(AK+CE=CM+CE=EM\).

Ta cần chứng minh \(EM=BE\) .

Xét \(\Delta BAK\) và \(\Delta BCM\) có:

\(AK=CM\) ( cách vẽ)

\(\begin{align} & \widehat{A}=\widehat{C}=90{}^\circ (gt) \\  & BA=BC(gt) \\  & \Rightarrow \Delta BAK=\Delta BCM(c.g.c) \\ \end{align}\)

\(\Rightarrow \widehat{ABK}=\widehat{CBM};\widehat{\,\,AKB}=\widehat{CMB}\) ( góc tương ứng)

Mà \(\widehat{ABK}=\widehat{KBE}\) (gt) nên \(\widehat{KBE}=\widehat{CBM}\) (bắc cầu).

Ta có:

\(\widehat{EBM}=\widehat{EBC}+\widehat{CBM}=\widehat{EBC}+\widehat{KBE}=\widehat{KBC}=\widehat{AKB}(slt)=\widehat{CMB}\)

Suy ra tam giác EBM cân tại E (định nghĩa tam giác cân).

 \(\begin{align}  & \Rightarrow BE=EM \\  & \Rightarrow AK+CE=CM+CE=EM=BE \\  & \Rightarrow AK+CE=BE\,\,\,\,\left( dpcm \right). \\ \end{align}\)