Câu hỏi
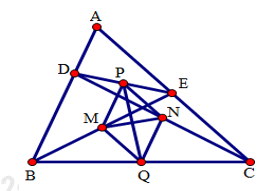
Cho tam giác ABC. Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE. Gọi M, P, N, Q thứ tự là trung điểm của BE, CD, DE và BC. Chứng minh PQ vuông góc với MN.
Phương pháp giải:
+ Để chứng minh \(MN \bot PQ\) trước hết ta chứng minh MNPQ là hình thoi dựa vào dấu hiệu tứ giác có bốn canh bằng nhau là hình thoi.
+ Ta nhận xét thấy MN, PQ là hai đường chéo của hình thoi nên \(MN \bot PQ\)
Lời giải chi tiết:
Từ giả thiết ta có MN, NP, NQ, QM lần lượt là các đường trung bình của các tam giác BDE, ECD, DCB, BEC. (định nghĩa đường trung bình).
Đặt BD = CE =2a.
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
\(MP = {1 \over 2}BD = a;NQ = {1 \over 2}DB = a;NP = {1 \over 2}CE = a;MQ = {1 \over 2}CE = a\)
Suy ra MN = NP = PQ = QM.
Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi MNPQ ta được: \(MN \bot PQ\) (đpcm).