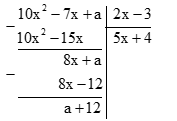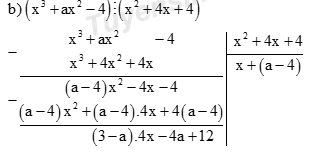Câu hỏi
Xác định hằng số a sao cho:
\(a)\;\left( {10{x^2} - 7x + a} \right) \vdots \left( {2x - 3} \right)\) \(b)\;\left( {{x^3} + a{x^2} - 4} \right) \vdots \left( {{x^2} + 4x + 4} \right)\)
- A a) - 12
b) 3
- B a) 12
b) 3
- C a) - 12
b)- 3
- D a) - 12
b) - 5
Phương pháp giải:
- Đặt phép chia.
- Để phép chia hết thì số dư cuối cùng phải bằng 0, từ đó ta tìm được a.
Lời giải chi tiết:
\(a)\;\left( {10{x^2} - 7x + a} \right) \vdots \left( {2x - 3} \right)\)
Để \(10{x^2} - 7x + a\) chia hết cho 2x - 3 thì \(a + 12 = 0 \Leftrightarrow a = - 12\)
Để \({x^3} + a{x^2}-4\) chia hết cho \({x^2} + 4x + 4\) thì \(\left( {3-a} \right).4x-4a + 12 = 0 \Leftrightarrow \left\{ \matrix{3 - a = 0 \hfill \cr 12 - 4a = 0 \hfill \cr} \right. \Leftrightarrow a = 3\)
Câu hỏi trước
