Câu hỏi
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, \(AB=a,AC=a\sqrt{3}\), cạnh bên SA vuông góc với đáy, \(SA=2\text{a}\). Khẳng định nào sau đây sai?
- A Diện tích tam giác SBC bằng \(\dfrac{{{a}^{2}}\sqrt{10}}{2}\)
- B Thể tích khối chóp S.ABC bằng \(\dfrac{{{a}^{3}}\sqrt{3}}{3}\)
- C Chiều cao của hình chóp kẻ từ đỉnh A bằng \(\dfrac{2a\sqrt{5}}{5}\)
- D Hình chóp có tất cả các mặt bên đều là tam giác vuông
Phương pháp giải:
Thể tích khối chóp \(V=\dfrac{1}{3}{{S}_{d}}.h=\dfrac{1}{3}SA.{{S}_{ABC}}\)
Lời giải chi tiết:
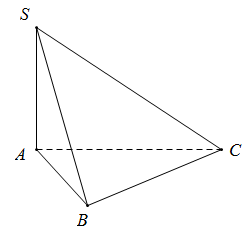
Khối chóp S.ABC có diện tích đáy \({{S}_{ABC}}=\frac{1}{2}AB.BC=\frac{1}{2}AB\sqrt{A{{C}^{2}}-A{{B}^{2}}}=\frac{{{a}^{2}}\sqrt{2}}{2}\) và thể tích
\(V=\frac{1}{3}SA.{{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{2}}{3}\)
Chọn đáp án B.
Câu hỏi trước
