Phương pháp giải:

Phương  pháp:

Câu a: Thay tọa độ của điểm A vào hàm số đã cho để tìm giá trị của m.

Vẽ đồ thị hàm số: Tìm ít nhất hai điểm thuộc đồ thị hàm số sau đó vẽ đường thẳng đi qua hai điểm đó.

Câu b: Đường thẳng \({{d}_{1}}\) căt \({{d}_{2}}\) tai 1 điểm trên trục hoành thì ta có giao điểm là \(M\left( {{x}_{0}};0 \right).\)

Thay điểm M vào phương trình đường thẳng \({{d}_{2}}\) ta được tọa độ điểm M. Sau đó ta thay tọa độ điểm M vào phương trình đường thẳng \({{d}_{1}}\) ta tìm được M.

Lời giải chi tiết:

Giải:

a) Đồ thị hàm số y = 2x +m - 1 đi qua điểm A(2;2) khi và chỉ khi

     2 = 2.2 + m – 1

 \(\Leftrightarrow \)m = -1.

Khi m = -1 hàm số trở thành y = 2x – 2

Cho x = 0 \(\Rightarrow \) y= 2.0 – 2 = -2

Điểm B(0; -2) thuộc đồ thị của hàm số y = 2x - 2

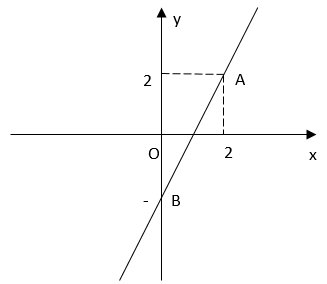
Đồ thị của hàm số y = 2x – 2 là đường thẳng đi qua hai điểm A(2;2) và B(0;-2)

Vẽ đồ thị của hàm số

b) Gọi M là giao điểm của đường thẳng \(y=2x+m-1\) và \(y=x+1.\)

Theo đề bài ta có M thuộc trục hoành \(\Rightarrow M\left( {{x}_{0}};0 \right).\)

M thuộc đường thẳng \(y=x+1\Rightarrow 0={{x}_{0}}+1\Leftrightarrow {{x}_{0}}=-1\Rightarrow M\left( -1;0 \right).\)

M thuộc đường thẳng \(y=2x+m-1\Rightarrow 0=2.\left( -1 \right)+m-1\Leftrightarrow m=3.\)

Vậy với m =  3 thì đồ thị của hàm số y = 2x + m – 1 cắt đồ thị của hàm số y = x +1 tại điểm nằm trên trục hoành.