Câu hỏi
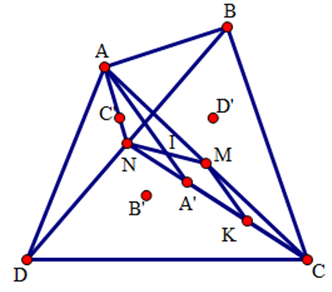
Cho tứ giác lồi \(ABCD,\) gọi \(A',\,B',\,C',\,D'\) lần lượt là trọng tâm của các tam giác \(BCD, \,ACD,\,ABD,\,ABC\) và \(M,\,N\) lần lượt là trung điểm của các đoạn thẳng \(AC,\,BD.\)
Chứng minh rằng các đường thẳng \(AA',\,BB',\,CC',\,DD'\) và \(MN\) đồng quy.
Phương pháp giải:
Dựa vào hình vẽ ta dự đoán \(AA',BB',CC',DD',MN\) sẽ đồng quy tại trung điểm của \(MN\). Gọi \(I\) là giao điểm của \(AA'\) và \(MN\) ta sẽ chứng minh \(I\) là trung điểm của \(MN\).
Ta dùng kiến thức về đường trung bình của tam giác và điểm \(K\) là trung điểm của \(A'C\) sẽ giúp ta giải bài toán.
Lời giải chi tiết:
Gọi \(I\) là giao điểm của \(AA'\) và \(MN,K\) là trung điểm của đoạn \(A'C\) .
Do \(A'\) là trọng tâm của tam giác \(BCD\) nên suy ra \(CK=KA=A'N\).
Tam giác \(AA'C\) có \(AM=MC\left( gt \right),CK=KA'\) suy ra \(MK\) là đường trung bình của tam giác \(AA'C.\)
Suy ra \(MK//AA'.\)
Tam giác \(NMK\) có \(IA'//MK\) và \(KA'=\text{ }A'N\) nên \(MI=IN\) .
Vậy \(I\) là trung điểm của \(MN,\) suy ra \(AA'\) đi qua trung điểm \(I\) của \(MN.\)
Chứng minh tương tự ta cũng có \(BB',CC',DD'\) đi qua \(I\).
Vậy các đường thẳng \(AA',\,BB',\,CC',\,DD',\,MN\) đồng quy.