Phương pháp giải:

Phương pháp giải. Lấy \(G,H,I,J\) lần lượt là trung điểm \(AB,\,BC,\,CD,\,DA.\) Sử dụng giả thiết để chứng minh Hình chóp \(S.ABCD$\) có các mặt đối xứng là \(\left( {SAC} \right),\,\left( {SBD} \right),\,\left( {SGI} \right),\,\left( {SHJ} \right).\)

Lời giải chi tiết:

Lời giải chi tiết.

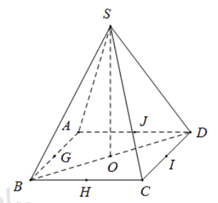
Giả sử \(S.ABCD\) là hình chóp tứ giác đều. Khi đó  đáy \(ABCD\) là hình vuông. Ta có hình chiếu của đỉnh \(S\) trùng với tâm của đáy \(ABCD\)

Hình chóp \(S.ABCD\) có các mặt đối xứng là \(\left( {SAC} \right),\,\left( {SBD} \right),\,\left( {SGI} \right),\,\left( {SHJ} \right)\) trong đó \(G,H,I,J\) lần lượt là trung điểm \(AB,\,BC,\,CD,\,DA.\)

Chọn đáp án D.