Câu hỏi
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác cân tại \(C\), cạnh bên \(SA\) vuông góc với đáy. Gọi \(H,K\) lần lượt là trung điểm của \(AB\) và \(SB\). Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
- A \(CH \bot SB\)
- B \(CH \bot AK\)
- C \(AK \bot BC\)
- D \(HK \bot HC\)
Lời giải chi tiết:
Phương pháp: Ta chứng minh \(CH \bot \left( {SAB} \right)\)
Cách giải
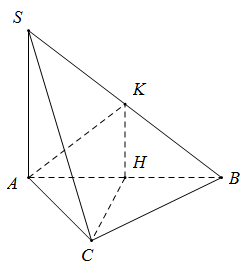
Vì \(\Delta ABC\) cân tại \(C\) mà \(H\) là trung điểm \(AB\) nên \(CH \bot AB\)
Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CH\)
Từ đó suy ra \(CH \bot \left( {SAB} \right)\)
\( \Rightarrow CH \bot SB\) và \(CH \bot HK\)
Vậy chỉ có mệnh đề \(AK \bot BC\) là sai
Chọn đáp án C







