Câu hỏi
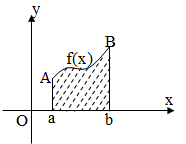
Cho hàm số \(f\left( x \right)\) liên tục và không âm trên đoạn \(\left[ {a;\,b} \right]\). Diện tích của hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,\,\,x = b\) được tính theo công thức nào dưới đây? (Hình dưới)
- A \(S = \pi \int_a^b {f\left( x \right)dx} \)
- B \(S = \pi \int_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \)
- C \(S = - \int_a^b {f\left( x \right)dx} \)
- D \(S = \int_a^b {f\left( x \right)dx} \)
Phương pháp giải:
Tính chất của tích phân.
Diện tích hình giới hạn bởi đồ thị \(y = f\left( x \right)\) với trục hoành và các đường thẳng \(x = a;x = b\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)
Lời giải chi tiết:
\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)\( = \int\limits_a^b {f\left( x \right)dx} \) do \(f\left( x \right) > 0\forall x \in \left[ {a;b} \right]\).







