Câu hỏi
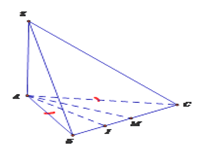
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), cạnh bên \(SA\) vuông góc với đáy, \(M\) là trung điểm của \[BC\], \(J\) là trung điểm của \(BM\). Mệnh đề nào sau đây là đúng?
- A \(BC \bot \left( {SAB} \right)\).
- B \(BC \bot \left( {SAJ} \right)\).
- C \(BC \bot \left( {SAC} \right)\)
- D \(BC \bot \left( {SAM} \right)\).
Phương pháp giải:
Tính chất tam giác cân: Đường trung tuyến kẻ từ đỉnh là đường cao.
Đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với 2 đường thẳng cắt nhau trong mặt phẳng đó.
Lời giải chi tiết:
\(\Delta ABC\) cân tại A
\(\left. \begin{array}{l} \Rightarrow BC \bot AM\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right\}\)\( \Rightarrow BC \bot \left( {SAM} \right)\)
Câu hỏi trước
