Phương pháp giải:

Sử dụng lý thuyết:

- Cho hai đường thẳng chéo nhau \(a,b\). Mặt phẳng \(\left( P \right)\) chứa \(b\) và song song với \(a\). Khi đó, \(d\left( {a,b} \right) = d\left( {a,\left( P \right)} \right)\).

- Thể tích khối lăng trụ \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

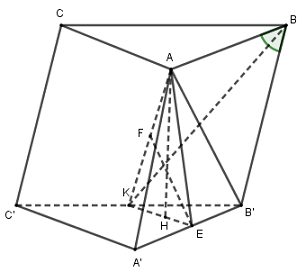
Tam giác \(AA'B\) có \(AA' = A'B\) và \(\widehat {A'} = \widehat B = {60^0}\) nên là tam giác đều cạnh \(2\).

Tam giác ABC vuông tại A có \(AB = 2,BC = 4\) nên theo Pitago ta có :

\(AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {{4^2} - {2^2}}  = 2\sqrt 3 \)\( \Rightarrow A'C' = AC = 2\sqrt 3 \).

Gọi E là trung điểm của A’B’ ta thấy,

AE là đường cao trong tam giác đều AA’B cạnh \(2\) nên \(AE = \dfrac{{2\sqrt 3 }}{2} = \sqrt 3 \)

KE là đường trung bình trong tam giác B’C’A’ nên \(KE = \dfrac{1}{2}A'C' = \dfrac{1}{2}.2\sqrt 3  = \sqrt 3 \)

Do đó tam giác AEK cân tại E.

Ta thấy, \(A'B'//AB \subset \left( {ABK} \right)\)\( \Rightarrow d\left( {A'B',BK} \right) = d\left( {A'B',\left( {ABK} \right)} \right)\) (1)

Mà \(AK \subset \left( {ABK} \right)\)\( \Rightarrow d\left( {A'B',AK} \right) = d\left( {A'B',\left( {ABK} \right)} \right)\) (2)

Từ (1) và (2) suy ra \(d\left( {A'B',BK} \right) = d\left( {A'B',AK} \right) = \dfrac{3}{2}\).

Gọi F là trung điểm của AK thì \(EF \bot AK\)  (3)

Lại có, \(\left\{ \begin{array}{l}AE \bot A'B'\\KE \bot A'B'\end{array} \right.\)\( \Rightarrow A'B' \bot \left( {AKE} \right) \Rightarrow A'B' \bot EF\) (4)

Do đó EF là đoạn vuông góc chung của hai đường thẳng A’B’ và AK \( \Rightarrow d\left( {A'B',AK} \right) = EF = \dfrac{3}{2}\).

Tam giác AEF vuông tại F có \(AE = \sqrt 3 ,EF = \dfrac{3}{2}\) nên theo Pitago ta có :

\(AF = \sqrt {A{E^2} - E{F^2}}  = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{3}{2}} \right)}^2}}  = \dfrac{{\sqrt 3 }}{2}\)\( \Rightarrow AK = 2AF = 2.\dfrac{{\sqrt 3 }}{2} = \sqrt 3 \)

Tam giác AKE có \(AE = EK = AK = \sqrt 3 \) nên là tam giác đều.

Gọi H là hình chiếu của A lên KE thì :

\(AH \bot KE\) và \(AH = EF = \dfrac{3}{2}\) (đường cao trong tam giác đều cạnh \(\sqrt 3 \)).

Mà \(A'B' \bot \left( {AKE} \right) \Rightarrow A'B' \bot AH\)

Do đó \(AH \bot \left( {A'B'C'} \right)\).

Vậy \({V_{ABC.A'B'C'}} = {S_{ABC}}.AH = \dfrac{1}{2}AB.AC.AH\)\( = \dfrac{1}{2}.2.2\sqrt 3 .\dfrac{3}{2} = 3\sqrt 3 \).

Chọn C.