Câu hỏi
Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\) có cạnh \(AB = 3\), \(BC = 4\)và góc giữa \(DC\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích mặt cầu ngoại tiếp tứ diện.
- A \(V = \dfrac{{125\sqrt 3 }}{3}\pi \)
- B \(V = \dfrac{{25\sqrt 2 }}{3}\pi \)
- C \(V = \dfrac{{125\sqrt 2 }}{3}\pi \)
- D \(V = \dfrac{{5\sqrt 2 }}{3}\pi \)
Phương pháp giải:
- Chứng minh tam giác \(BCD\) vuông tại \(B\), từ đó tìm tâm mặt cầu ngoại tiếp tứ diện.
- Xác định góc giữa \(DC\) và \(\left( {ABC} \right)\) là góc giữa \(DC\) và hình chiếu của \(DC\) lên \(\left( {ABC} \right)\).
- Sử dụng định lí Pytago, tính chất tam giác vuông cân tính bán kính mặt cầu.
- Tính thể tích khối cầu có bán kính R là : \(V = \dfrac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
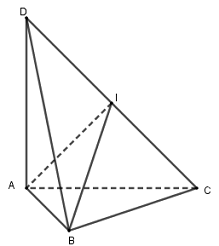
Ta có : \(\left\{ \begin{array}{l}BC \bot BA\\BC \bot DA\end{array} \right. \Rightarrow BC \bot \left( {ABD} \right)\)\( \Rightarrow BC \bot BD\)\( \Rightarrow \Delta BCD\) vuông tại B.
Gọi I là trung điểm của CD thì \(IB = IC = ID = \dfrac{1}{2}CD\).
Tam giác ACD vuông tại A nên \(IA = IC = ID = \dfrac{1}{2}CD\).
Do đó \(IA = IB = IC = ID \Rightarrow I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).
Tam giác ABC vuông tại B nên \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (Định lí Pytago).
Vì \(DA \bot \left( {ABC} \right)\) nên \(AC\) là hình chiếu của \(DC\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {DC;\left( {ABC} \right)} \right) = \angle \left( {DC;AC} \right) = \angle DCA = {45^0}\).
Tam giác \(DAC\) vuông tại \(A\) có \(\widehat {DCA} = {45^0}\) nên là tam giác vuông cân \( \Rightarrow DC = AC\sqrt 2 = 5\sqrt 2 \).
\( \Rightarrow R = IA = \dfrac{1}{2}DC = \dfrac{{5\sqrt 2 }}{2}\).
Vậy thể tích khối cầu ngoại tiếp tứ diện \(ABCD\) là : \(V = \dfrac{4}{3}\pi I{A^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{5\sqrt 2 }}{2}} \right)^3} = \dfrac{{125\sqrt 2 }}{3}\pi \).
Chọn C.







