Phương pháp giải:

- Tam giác \(OAB\) cân nên sẽ vuông cân tại \(O\).

- Sử dụng định nghĩa hệ số góc của đường thẳng \(y = ax + b\) là \(a = \tan \alpha \), với \(\alpha \) là góc tạo bởi đường thẳng và chiều dương của trục \(Ox\).

Lời giải chi tiết:

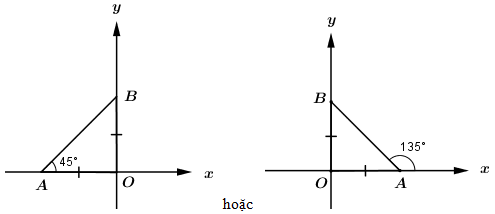
Tam giác \(OAB\) cân (gt), lại có \(\Delta OAB\) vuông tại \(O\), suy ra \(\Delta OAB\) vuông cân tại \(O\), do đó đường thẳng \(y = mx + 3\) tạo với chiều dương trục \(Ox\) hoặc góc \({45^0}\), hoặc góc \({135^0}\).

\( \Rightarrow \left[ \begin{array}{l}m = \tan {45^0}\\m = \tan {135^0}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\) \( \Rightarrow S = \left\{ { - 1;1} \right\}\).

Vậy tổng các phần tử của \(S\) là \( - 1 + 1 = 0\).

Chọn D.