Câu hỏi
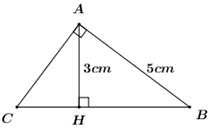
Trong hình vẽ bên, tam giác \(ABC\) vuông tại \(A,\) cạnh \(AB = 5cm,\) đường cao \(AH = 3cm.\) Độ dài cạnh \(BC\)bằng
- A \(\dfrac{4}{{15}}\,cm.\)
- B \(4cm.\)
- C \(\dfrac{{25}}{4}cm.\)
- D \(\dfrac{{25}}{{16}}cm.\)
Phương pháp giải:
- Áp dụng định lý Pytago trong tam giác vuông \(AHB\) tính \(BH\).
- Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính \(BC\): \(A{B^2} = BH.BC\).
Lời giải chi tiết:
Áp dụng định lý Pytago trong tam giác vuông \(AHB\) ta có:
\(\begin{array}{l}B{H^2} = A{B^2} - A{H^2}\\B{H^2} = {5^2} - {3^2}\\B{H^2} = 16\\ \Rightarrow BH = 4\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\) \( \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{5^2}}}{4} = \dfrac{{25}}{4}\,\,\left( {cm} \right)\).
Chọn C.