Phương pháp giải:

- Đánh giá, chặn khoảng giá trị của biểu thức \(A.\)

- Tìm các giá trị nguyên của \(A\) trong khoảng hoặc đoạn bị chặn, từ đó tìm \(x\) và đối chiếu điều kiện.

Lời giải chi tiết:

Với \(x \ge 0\), ta có: \(A = \dfrac{{4\sqrt x  + 16}}{{\sqrt x  + 2}} = \dfrac{{4\left( {\sqrt x  + 2} \right) + 8}}{{\sqrt x  + 2}} = 4 + \dfrac{8}{{\sqrt x  + 2}}\).

Vì \(\sqrt x  + 2 \ge 2\) nên \(\dfrac{8}{{\sqrt x  + 2}} \le 4\) \( \Rightarrow A = 4 + \dfrac{8}{{\sqrt x  + 2}} \le 8\).

Lại có \(\dfrac{8}{{\sqrt x  + 2}} > 0\) nên \(A = 4 + \dfrac{8}{{\sqrt x  + 2}} > 4\).

\( \Rightarrow 4 < A \le 8\).

Mà \(A\) nhận giá trị nguyên \( \Rightarrow A \in \left\{ {5;6;7;8} \right\}\) \( \Rightarrow \dfrac{8}{{\sqrt x  + 2}} \in \left\{ {1;2;3;4} \right\}\).

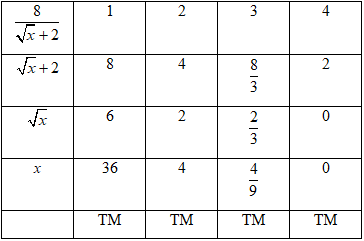
Ta có bảng sau:

Vậy có \(4\) giá trị của \(x\) để biểu thức \(A\) nhận giá trị nguyên.

Chọn B.