Câu hỏi
Tiến hành thí nghiệm với 2 con lắc lò xo A và B có quả nặng và chiều dài tự nhiên giống nhau với độ cứng lần lượt là k và 2k. Hai con lắc được treo thẳng đứng vào cùng một giá đỡ. Kéo hai quả nặng đến cùng một vị trí ngang nhau rồi thả nhẹ cùng lúc. Năng lượng dao động của con lắc B gấp 8 lần năng lượng dao động của con lắc A. Gọi tA, tBlà khoảng thời gian ngắn nhất kể từ lúc bắt đầu thả hai vật đến khi lực đàn hồi của mỗi con lắc có độ lớn nhỏ nhất. Tỷ số \(\frac{{{t_B}}}{{{t_A}}}\) là:
- A \(\frac{{\sqrt 2 }}{3}\)
- B \(\frac{3}{2}\)
- C \(\frac{{3\sqrt 2 }}{2}\)
- D \(\frac{3}{{2\sqrt 2 }}\)
Phương pháp giải:
Xác định độ dãn ban đầu của mỗi lò xo:
\(\Delta {l_0} = \frac{{mg}}{k}\)
Áp dụng công thức cơ năng
\({\rm{W}} = \frac{1}{2}.k.{A^2}\)
Lực đàn hồi:
\(F = k.\left| {\Delta l} \right|\)
Chu kì dao động của con lắc lò xo:
\(T = 2\pi \sqrt {\frac{m}{k}} \)
Sử dụng VTLG để xác định thời gian từ vị trí ban đầu đến vị trí lò xo không dãn và tìm tỉ số.
Lời giải chi tiết:
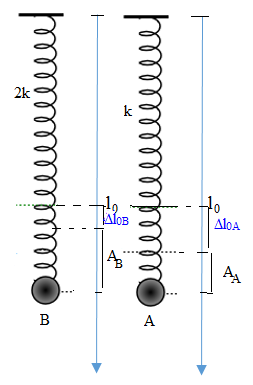
Độ dãn ban đầu của lò xo A là \(\Delta {l_{0A}} = \frac{{mg}}{k}\)
Độ dãn ban đầu của lò xo B là \(\Delta {l_{0B}} = \frac{{mg}}{{2k}} = \frac{1}{2}\Delta {l_{0A}}\)
Áp dụng công thức cơ năng:
\(\left\{ \begin{array}{l}
{{\rm{W}}_A} = \frac{1}{2}.k.A_A^2\\
{{\rm{W}}_B} = \frac{1}{2}.2k.A_B^2
\end{array} \right. \Rightarrow \frac{{{\rm{W}}{}_B}}{{{{\rm{W}}_A}}} = \frac{{2A_B^2}}{{A_A^2}} = 8 \Rightarrow {A_B} = 2{A_A}\)
Từ hình vẽ ta thấy:
\(\begin{array}{l}
\Delta {l_B} + {A_B} = \Delta {l_A} + {A_A} \Leftrightarrow \Delta {l_B} + 2{A_A} = 2\Delta {l_B} + {A_A}\\
\Leftrightarrow {A_A} = \Delta {l_B} = \frac{1}{2}\Delta {l_A} \Rightarrow {A_B} = 2{A_A} = 2\Delta {l_B}
\end{array}\)
Chu kì dao động của con lắc lò xo A:
\({T_A} = 2\pi \sqrt {\frac{m}{k}} \)
Chu kì dao động của con lắc lò xo B:
\({T_B} = 2\pi \sqrt {\frac{m}{{2k}}} = \frac{{{T_A}}}{{\sqrt 2 }}\)
Ta thấy biên độ của A nhỏ hơn độ dãn ban đầu của lò xo, vì vậy lực đàn hồi của lò xo luôn lò là lực kéo và có giá trị nhỏ nhất tại biên âm. Ban đầu vật ở biên dương, nên \({t_A} = \frac{{{T_A}}}{2}\)
Lò xo B có biên độ lớn hơn độ dãn ban đầu, nên lực đàn hồi nhỏ nhất = 0 tại vị trí lò xo không dãn. Ta có VTLG:
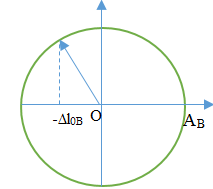
Thời gian:
\({t_B} = \frac{{\frac{\pi }{2} + {\rm{ar}}\cos \frac{{\Delta {l_B}}}{{{A_B}}}}}{{2\pi }}.{T_B} = \frac{{{T_B}}}{3} = \frac{{{T_A}}}{{3\sqrt 2 }}\)
Ta có tỉ số:
\(\frac{{{t_B}}}{{{t_A}}} = \frac{{\frac{{{T_A}}}{{3\sqrt 2 }}}}{{\frac{{{T_A}}}{2}}} = \frac{{\sqrt 2 }}{3}\)
Chọn A.







