Phương pháp giải:

- Xác định bán kính mặt cầu ngoại tiếp chóp là giao điểm của hai trục của hai mặt bất kì.

- Sử dụng tam giác đồng dạng để tính bán kính mặt cầu.

Lời giải chi tiết:

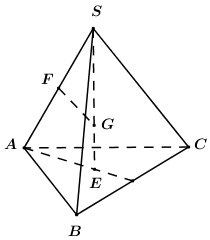
Gọi \(E\) là tâm tam giác đều \(ABC\) \( \Rightarrow SE \bot \left( {ABC} \right)\) và \(SE\) là trục của \(\left( {ABC} \right)\).

Gọi \(F\) là trung điểm của \(SA\). Trong \(\left( {SAE} \right)\), từ \(F\) kẻ đường thẳng vuông góc với \(SA\) và cắt \(SE\) tại \(G\).

Ta có: \(\left\{ \begin{array}{l}G \in SE \Rightarrow GA = GB = GC\\G \in GF \Rightarrow GS = GA\end{array} \right.\) \( \Rightarrow GA = GB = GC = GS\), do đó \(G\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).

Xét \(\Delta SFG\) và \(\Delta SEA\) có: \(\angle ASE\) chung, \(\angle SFG = \angle SEA = {90^0}\).

\( \Rightarrow \Delta SFG \sim \Delta SEA\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{SF}}{{SE}} = \dfrac{{SG}}{{SA}}\) \( \Rightarrow SG = \dfrac{{SA.SF}}{{SE}} = \dfrac{{b.\dfrac{b}{2}}}{h} = \dfrac{{{b^2}}}{{2h}}\).

Vậy bán kính mặt cầu ngoại tiếp khối chóp \(S.ABC\) là \(R = SG = \dfrac{{{b^2}}}{{2h}}\).

Chọn C.