Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\), \(\angle ABC = {120^0}\). \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) bằng \({60^0}\), khi đó:
- A \(SA = \dfrac{{a\sqrt 6 }}{4}\)
- B \(SA = a\sqrt 6 \)
- C \(SA = \dfrac{{a\sqrt 6 }}{2}\)
- D \(SA = \dfrac{{a\sqrt 3 }}{2}\)
Phương pháp giải:
- Trong \(\left( {SBC} \right)\) kẻ \(BH \bot SC\,\,\left( {H \in SC} \right)\), chứng minh \(DH \bot SC\) và suy ra \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BH;DH} \right)\)
- Xét 2 trường hợp \(\widehat {BHD} = {60^0}\) hoặc \(\angle BHD = {120^0}\).
- Chứng minh \(\Delta BDH\) cân tại \(H\), từ đó tính \(HO\) theo \(a\) với \(O = AC \cap BD\).
- Chứng minh \(\Delta SAC \sim \Delta OHC\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{SA}}{{OH}} = \dfrac{{SC}}{{OC}}\). Giải phương trình tìm \(SA\) theo \(a\).
Lời giải chi tiết:
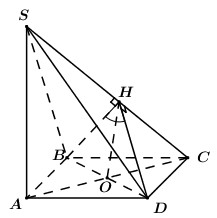
Gọi \(O = AC \cap BD\), do \(ABCD\) là hình thoi nên \(AC \bot BD\) tại \(O\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\).
Trong \(\left( {SBC} \right)\) kẻ \(BH \bot SC\,\,\left( {H \in SC} \right)\) ta có: \(\left\{ \begin{array}{l}SC \bot BH\\SC \bot BD\end{array} \right. \Rightarrow SC \bot \left( {BDH} \right) \Rightarrow SC \bot DH\).
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\BH \subset \left( {SBC} \right),\,\,BH \bot SC\\DH \subset \left( {SCD} \right),\,\,DH \bot SC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BH;DH} \right) = {60^0}\)
\( \Rightarrow \widehat {BHD} = {60^0}\) hoặc \(\angle BHD = {120^0}\).
Xét \(\Delta ABD\) có \(AB = AD = a\), \(\angle BAD = {180^0} - \angle ABC = {60^0}\) (hai góc trong cùng phía bù nhau) \( \Rightarrow \Delta ABD\) đều cạnh \(a\) \( \Rightarrow BD = a,\,\,AO = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow BO = \dfrac{1}{2}BD = \dfrac{a}{2}\).
Xét \(\Delta SAB\) và \(\Delta SAD\) có:
\(\begin{array}{l}\angle SAB = \angle SAD = {90^0}\\SA\,\,chung\\AB = AD = a\end{array}\)
\( \Rightarrow \Delta SAB = \Delta SAD\) (2 cạnh góc vuông) \( \Rightarrow SB = SD\).
Xét \(\Delta SBC\) và \(\Delta SDC\) có:
\(\begin{array}{l}SB = SD\,\,\left( {cmt} \right)\\SC\,\,chung\\BC = DC = a\end{array}\)
\( \Rightarrow \Delta SBC = \Delta SDC\,\,\,\left( {c.c.c} \right)\)\( \Rightarrow BH = DH\) (2 đường cao tương ứng) \( \Rightarrow \Delta BDH\) cân tại \(H\) \( \Rightarrow HO\) là đường trung tuyến đồng thời là đường cao và đường phân giác \( \Rightarrow HO \bot BD\) và \(\angle BHO = \dfrac{1}{2}\angle BHD\).
Ta có: \(SC \bot \left( {BDH} \right)\,\,\left( {cmt} \right) \Rightarrow SC \bot OH\).
Xét \(\Delta SAC\) và \(\Delta OHC\) có: \(\angle SCA\) chung, \(\angle SAC = \angle OHC = {90^0}\), suy ra \(\Delta SAC \sim \Delta OHC\,\,\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{SA}}{{OH}} = \dfrac{{SC}}{{OC}} \Rightarrow SA = \dfrac{{OH.SC}}{{OC}}\,\,\left( * \right)\), với \(OC = OA = \dfrac{{a\sqrt 3 }}{2}\), \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + 3{a^2}} \).
TH1: \(\angle BHD = {60^0} \Rightarrow \angle BHO = {30^0}\).
Xét tam giác vuông \(BHO\) có: \(OH = BO.\cot {30^0} = \dfrac{{a\sqrt 3 }}{2} = OC\) (Vô lí do \(OH < OC\) - quan hệ đường vuông góc, đường xiên).
TH1: \(\angle BHD = {120^0} \Rightarrow \angle BHO = {60^0}\).
Xét tam giác vuông \(BHO\) có: \(OH = BO.\cot {60^0} = \dfrac{a}{2}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{6}\).
Thay vào (*) ta có:
\(\begin{array}{l}SA = \dfrac{{\dfrac{{a\sqrt 3 }}{6}.\sqrt {S{A^2} + 3{a^2}} }}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow SA = \dfrac{{\sqrt {S{A^2} + 3{a^2}} }}{3}\\ \Leftrightarrow 9S{A^2} = S{A^2} + 3{a^2} \Leftrightarrow 8S{A^2} = 3{a^2}\\ \Leftrightarrow S{A^2} = \dfrac{{3{a^2}}}{8} \Leftrightarrow SA = \dfrac{{a\sqrt 6 }}{4}\end{array}\)
Chọn A.







