Câu hỏi
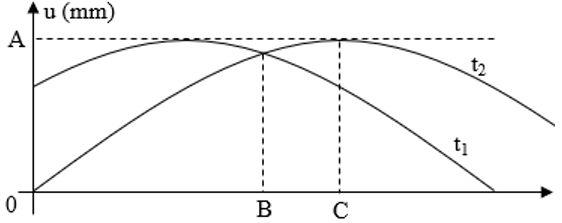
Trên một sợi dây dài, đang có sóng ngang truyền qua. Hình dạng của một đoạn dây tại hai thời điểm \({t_1}\) và \({t_2}\) như hình vẽ. Li độ của các phần tử tại B và C ở thời điểm \({t_1}\) lần lượt là \(10\sqrt 3 mm\) và\(10mm\). Biết \(\Delta t = {t_2} - {t_1} = \dfrac{{0,05}}{6}s\) và nhỏ hơn một chu kì sóng. Tốc độ dao động cực đại của các phần tử trên dây bằng
- A \(0,4\pi \sqrt 2 m/s\)
- B \(0,4\pi m/s\)
- C \(0,8\pi m/s\)
- D \(0,8\pi \sqrt 3 m/s\)
Phương pháp giải:
+ Đọc đồ thị
+ Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
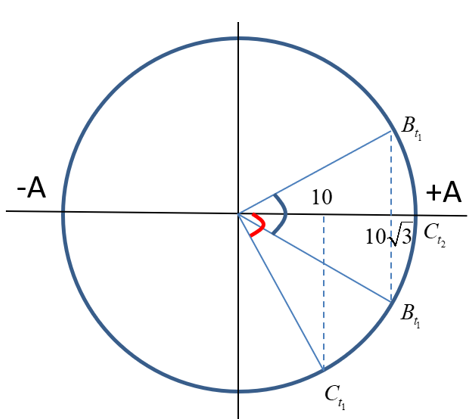
Từ đồ thị, xác định các điểm B, C tại thời điểm \({t_1},{t_2}\) trên vòng tròn lượng giác, ta có:
Ta có: \(\Delta {\varphi _{C\left( {{t_1} \to {t_2}} \right)}} = \Delta {\varphi _{B\left( {{t_1} \to {t_2}} \right)}} = \alpha = \omega .\Delta t\)
Từ vòng tròn lượng giác, ta có: \(\left\{ \begin{array}{l}cos\alpha = \dfrac{{10}}{A}\\cos\dfrac{\alpha }{2} = \dfrac{{10\sqrt 3 }}{A}\end{array} \right.\)
Từ đây ta suy ra \(cos\alpha = \dfrac{1}{2} \Rightarrow \alpha = {60^0} = \dfrac{\pi }{3}\)
\( \Rightarrow A = 20mm\)
Lại có: \(\alpha = \omega .\Delta t \Rightarrow \omega = \dfrac{\alpha }{{\Delta t}} = \dfrac{{\dfrac{\pi }{3}}}{{\dfrac{{0,05}}{6}}} = 40\pi \left( {rad/s} \right)\)
Tốc độ dao động cực đại của các phần tử dao động trên dây: \({v_{max}} = A\omega = 20.40\pi = 800\pi \left( {mm/s} \right) = 0,8\pi \left( {m/s} \right)\)
Chọn C