Câu hỏi
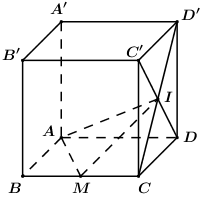
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\), điểm \(M\) là trung điểm cạnh \(BC\) và \(I\) là tâm hình vuông \(CDD'C'\). Mặt phẳng \(\left( {AMI} \right)\) chia khối lập phương thành hai khối đa diện, trong đó khối đa diện không chứa điểm \(D\) có thể tích là \(V\). Khi đó giá trị của \(V\) là:
- A \(V = \dfrac{7}{{36}}{a^3}\)
- B \(V = \dfrac{{22}}{{29}}{a^3}\)
- C \(V = \dfrac{7}{{29}}{a^3}\)
- D \(V = \dfrac{{29}}{{36}}{a^3}\)
Phương pháp giải:
- Xác định thiết diện của khối lập phương cắt bởi \(\left( {AMI} \right)\).
- Chứng minh \(V = {V_{ABCD.A'B'C'D'}} - {V_{CDAMNP}} = {a^3} - {V_1}\).
- Phân chia khối đa diện: \({V_1} = {V_{D.APE}} - {V_{C.MNE}}\).
- Sử dụng định lí Ta-lét, định lí Menelaus tính độ dài các cạnh, từ đó tính thể tích các khối tứ diên vuông \({V_{D.APE}};\,\,{V_{C.MNE}}\).
Lời giải chi tiết:
Trong \(\left( {ABCD} \right)\) kéo dài \(AM \cap CD = \left\{ E \right\}\). Trong \(\left( {CDD'C'} \right)\) kéo dài \(EI\) cắt \(CC',\,\,DD'\) lần lượt tại \(N,\,\,P\). Khi đó \(\left( {AMI} \right)\) cắt khối lập phương \(ABCD.A'B'C'D'\) theo thiết diện là tứ giác \(AMNP\) và thể tích khối đa diện không chứa điểm \(D\) là \(V = {V_{ABCD.A'B'C'D'}} - {V_{CDAMNP}} = {a^3} - {V_1}\).
Ta có \({V_1} = {V_{D.APE}} - {V_{C.MNE}}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{MC}}{{AD}} = \dfrac{{EM}}{{EA}} = \dfrac{{EC}}{{ED}} = \dfrac{1}{2}\) nên \(M,\,\,C\) lần lượt là trung điểm của \(AE\) và \(DE\).
Khi đó ta có \(CE = CD = a,\,\,DE = 2CD = 2a\).
Áp dụng định lí Menelaus trong tam giác \(DD'E\) có: \(\dfrac{{PD}}{{PD'}}.\dfrac{{ID'}}{{IC}}.\dfrac{{EC}}{{ED}} = 1\) \( \Leftrightarrow \dfrac{{PD}}{{PD'}}.1.\dfrac{1}{2} = 1 \Leftrightarrow \dfrac{{PD}}{{PD'}} = 2\).
\( \Rightarrow PD = \dfrac{2}{3}DD' = \dfrac{{2a}}{3}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{NC}}{{PD}} = \dfrac{{EC}}{{ED}} = \dfrac{1}{2}\) \( \Rightarrow NC = \dfrac{1}{2}PD = \dfrac{a}{3}\).
\(\begin{array}{l} \Rightarrow {V_{D.APE}} = \dfrac{1}{6}DP.DA.DE = \dfrac{1}{6}.\dfrac{{2a}}{3}.a.2a = \dfrac{{2{a^3}}}{9}\\\,\,\,\,\,\,{V_{C.MNE}} = \dfrac{1}{6}.CN.CM.CE = \dfrac{1}{6}.\dfrac{a}{3}.\dfrac{a}{2}.a = \dfrac{{{a^3}}}{{36}}\end{array}\)
\( \Rightarrow {V_1} = {V_{D.APE}} - {V_{C.MNE}} = \dfrac{{2{a^3}}}{9} - \dfrac{{{a^3}}}{{36}} = \dfrac{{7{a^3}}}{{36}}\).
Vậy \(V = {a^3} - {V_1} = {a^3} - \dfrac{{7{a^3}}}{{36}} = \dfrac{{29{a^3}}}{{36}}\).
Chọn D.