Câu hỏi
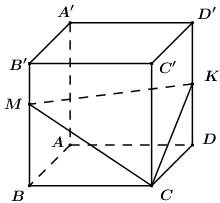
Cho khối lập phương \(ABCD.A'B'C'D'\) có độ dài một cạnh là \(a\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao \(BM = 2MB'\), \(K\) là trung điểm \(DD'\). Mặt phẳng \(\left( {CMK} \right)\) chia khối lập phương thành hai khối đa diện, tính theo \(a\) thể tích \({V_1}\) của khối đa diện chứa đỉnh \(C'\).
- A \({V_1} = \dfrac{{7{a^3}}}{{12}}\)
- B \({V_1} = \dfrac{{95{a^3}}}{{216}}\)
- C \({V_1} = \dfrac{{25{a^3}}}{{72}}\)
- D \({V_1} = \dfrac{{181{a^3}}}{{432}}\)
Phương pháp giải:
- Xác định thiết diện của hình lập phương cắt bởi \(\left( {CMK} \right)\).
- Phân chia và lắp ghép các khối đa diện.
Lời giải chi tiết:
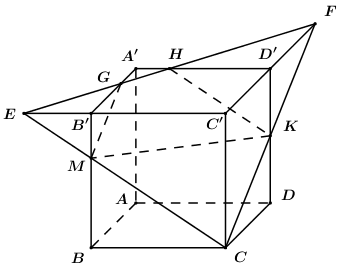
Trong \(\left( {BCC'B'} \right)\) kéo dài \(CM\) cắt \(B'C'\) tại \(E\), trong \(\left( {CDD'C'} \right)\) kéo dài \(CK\) cắt \(C'D'\) tại \(F\).
Trong \(\left( {A'B'C'D'} \right)\) nối \(EF\) cắt \(A'B',\,\,A'D'\) lần lượt tại \(G,\,\,H\).
Khi đó thiết diện của khối lập phương cắt bởi \(\left( {CMK} \right)\) là ngũ giác \(CMGHK\) và \({V_1} = {V_{C.C'EF}} - {V_{M.B'EG}} - {V_{K.D'HF}}\)
Áp dụng định lí Ta-lét ta có:
\(\dfrac{{EB'}}{{EC'}} = \dfrac{{B'M}}{{CC'}} = \dfrac{1}{3}\) \( \Rightarrow EB' = \dfrac{1}{3}EC' \Rightarrow EB' = \dfrac{1}{2}B'C' = \dfrac{a}{2}\).
\(\dfrac{{FD'}}{{FC'}} = \dfrac{{D'K}}{{CC'}} = \dfrac{1}{2}\) \( \Rightarrow D'\) là trung điểm của \(C'F\) nên \(C'F = 2a,\,\,D'F = a\).
\(\dfrac{{B'G}}{{C'F}} = \dfrac{{EB'}}{{EC'}} = \dfrac{1}{3}\) \( \Rightarrow B'G = \dfrac{1}{3}C'F = \dfrac{{2a}}{3}\) \( \Rightarrow A'G = A'B' - B'G = \dfrac{a}{3}\).
Ta có \(\dfrac{{EB'}}{{EC'}} = \dfrac{1}{3} \Rightarrow \dfrac{{B'C'}}{{EC'}} = \dfrac{2}{3} \Rightarrow EC' = \dfrac{{3a}}{2}\).
\(\dfrac{{HD'}}{{EC'}} = \dfrac{{FD'}}{{FC'}} = \dfrac{1}{2} \Rightarrow HD' = \dfrac{1}{2}EC' = \dfrac{{3a}}{4}\) \( \Rightarrow A'H = A'D' - HD' = \dfrac{a}{4}\).
Khi đó ta có:
\({S_{C'EF}} = \dfrac{1}{2}C'E.C'F = \dfrac{1}{2}.\dfrac{{3a}}{2}.2a = \dfrac{{3{a^2}}}{2}\) \( \Rightarrow {V_{C.C'EF}} = \dfrac{1}{3}CC'.{S_{C'EE}} = \dfrac{1}{3}.a.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}}}{2}\).
\({S_{B'EG}} = \dfrac{1}{2}B'E.B'G = \dfrac{1}{2}.\dfrac{a}{2}.\dfrac{{2a}}{3} = \dfrac{{{a^2}}}{6}\) \( \Rightarrow {V_{M.B'EG}} = \dfrac{1}{3}MB'.{S_{B'EG}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{6} = \dfrac{{{a^3}}}{{54}}\).
\({S_{D'HF}} = \dfrac{1}{2}D'H.D'F = \dfrac{1}{2}.\dfrac{{3a}}{4}.a = \dfrac{{3{a^2}}}{8}\)\( \Rightarrow {V_{K.D'HF}} = \dfrac{1}{3}.KD'.{S_{D'HF}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{3{a^2}}}{8} = \dfrac{{{a^3}}}{{16}}\).
Vậy \({V_1} = {V_{C.C'EF}} - {V_{M.B'EG}} - {V_{K.D'HF}} = \dfrac{{{a^3}}}{2} - \dfrac{{{a^3}}}{{54}} - \dfrac{{{a^3}}}{{16}} = \dfrac{{181{a^3}}}{{432}}\).
Chọn D.







