Câu hỏi
Dòng điện chạy qua một đoạn mạch có biểu thức \(i = {I_0}\sin 100\pi t\). Trong khoảng thời gian từ \(0\) đến \(0,01\,\,s\), cường độ dòng điện tức thời có giá trị bằng \(0,5{I_0}\) vào những thời điểm
- A \(\dfrac{1}{{600}}\,\,s\) và \(\dfrac{5}{{600}}\,\,s\).
- B \(\dfrac{1}{{500}}\,\,s\) và \(\dfrac{3}{{500}}\,\,s\).
- C \(\dfrac{1}{{300}}\,\,s\) và \(\dfrac{2}{{300}}\,\,s\).
- D \(\dfrac{1}{{400}}\,\,s\) và \(\dfrac{2}{{400}}\,\,s\).
Phương pháp giải:
Chu kì của dòng điện: \(T = \dfrac{{2\pi }}{\omega }\)
Sử dụng vòng tròn lượng giác và công thức: \(t = \dfrac{\varphi }{\omega }\)
Lời giải chi tiết:
Phương trình cường độ dòng điện:
\(i = {I_0}\sin \omega t = {I_0}\cos \left( {\omega t - \dfrac{\pi }{2}} \right)\)
Pha ban đầu của cường độ dòng điện là: \( - \dfrac{\pi }{2}\)
Chu kì của dòng điện là: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{100\pi }} = 0,02\,\,\left( s \right)\)
Trong thời gian \(0,01\,\,s\), dòng điện thực hiện được số chu kì là:
\(\dfrac{t}{T} = \dfrac{{0,01}}{{0,02}} = \dfrac{1}{2} \Rightarrow t = \dfrac{T}{2}\)
Ta có vòng tròn lượng giác:
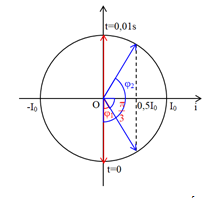
Từ vòng tròn lượng giác, ta thấy từ thời điểm đầu, cường độ dòng điện có giá trị \(0,5{I_0}\) khi vecto quay được các góc:
\(\left\{ \begin{array}{l}{\varphi _1} = \dfrac{\pi }{2} - \dfrac{\pi }{3} = \dfrac{\pi }{6}\,\,\left( {rad} \right) \Rightarrow {t_1} = \dfrac{{{\varphi _1}}}{\omega } = \dfrac{1}{{600}}\,\,\left( s \right)\\{\varphi _2} = \dfrac{\pi }{2} + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6}\,\,\left( {rad} \right) \Rightarrow {t_2} = \dfrac{{{\varphi _2}}}{\omega } = \dfrac{5}{{600}}\,\,\left( s \right)\end{array} \right.\)
Chọn A.







