Câu hỏi
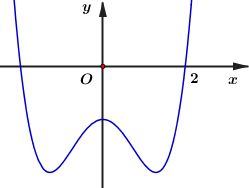
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ. Mệnh đề nào sau đây sai?
- A \(a + b + c < 0\)
- B \(a > 0\)
- C \(b > 0\)
- D \(c < 0\)
Phương pháp giải:
Dựa vào số điểm cực trị và các điểm mà đồ thị hàm số đi qua để chọn đáp án đúng.
Cho hàm số \(y = a{x^4} + b{x^2} + c\,\,\left( {a \ne 0} \right)\) ta có:
+) Hàm số có một cực trị \( \Leftrightarrow ab \ge 0\)
+) Hàm số có ba cực trị \( \Leftrightarrow ab < 0\)
+) Hàm số có đúng một cực trị và cực trị là cực tiểu \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\b \ge 0\end{array} \right.\)
+) Hàm số có đúng một cực trị và cực trị là cực đại \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\b \le 0\end{array} \right.\)
+) Hàm số có hai cực tiểu và một cực đại \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\b < 0\end{array} \right.\)
+) Hàm số có một cực tiểu và hai cực đại \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\b > 0\end{array} \right.\)
Lời giải chi tiết:
Ta thấy đồ thị hàm số cắt trục tung tại điểm có tung độ âm \( \Rightarrow c < 0\) \( \Rightarrow \) Đáp án D đúng.
Dựa vào đồ thị hàm số ta thấy hàm số đã cho có 3 điểm cực trị, trong đó có 2 điểm cực tiểu và 1 điểm cực đại
\( \Rightarrow \left\{ \begin{array}{l}a > 0\\b < 0\end{array} \right. \Rightarrow \) Đáp án C sai.
Chọn C.







