Câu hỏi
Cho hàm số \(y = f\left( x \right) = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ:
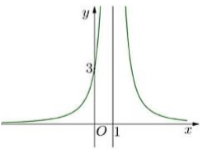
Biết đồ thị hàm số \(y = f\left( x \right)\) đi qua điểm \(\left( {0;1} \right)\). Giá trị \(f\left( { - 2} \right)\) bằng:
- A \( - 1\)
- B \(3\)
- C \(1\)
- D \( - 3\)
Phương pháp giải:
- Dựa vào đồ thị hàm số \(f'\left( x \right)\) đi qua \(\left( {0;3} \right)\) tính \(a\) theo \(c\). Từ đó suy ra hàm số \(f\left( x \right)\).
- Thay \(x = - 2\) tính \(f\left( { - 2} \right)\).
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - \dfrac{d}{c}} \right\}\).
Đồ thị hàm số đi qua điểm \(\left( {0;1} \right)\) \( \Rightarrow 1 = \dfrac{b}{d} \Leftrightarrow b = d\).
Ta có \(f'\left( x \right) = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\).
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\), ta thấy hàm số không xác định tại \(x = 1\).
\( \Rightarrow - \dfrac{d}{c} = 1 \Leftrightarrow d = - c = b\).
Lại có đồ thị hàm số \(y = f'\left( x \right)\) đi qua điểm \(\left( {0;3} \right)\) \( \Rightarrow 3 = \dfrac{{ad - bc}}{{{d^2}}}\).
\(\begin{array}{l} \Rightarrow 3 = \dfrac{{a.\left( { - c} \right) - \left( { - c} \right).c}}{{{{\left( { - c} \right)}^2}}} \Leftrightarrow - ac + {c^2} = 3{c^2}\\ \Leftrightarrow 2{c^2} + ac = 0 \Leftrightarrow c\left( {2c + a} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}c = 0\\a = - 2c\end{array} \right.\end{array}\)
Với \(c = 0 \Rightarrow b = d = 0\) (Loại) \( \Rightarrow c \ne 0\).
Với \(a = - 2c\), hàm số có dạng \(y = f\left( x \right) = \dfrac{{ - 2cx - c}}{{cx - c}} = \dfrac{{ - 2x - 1}}{{x - 1}}\).
Vậy \(f\left( { - 2} \right) = \dfrac{{ - 2.\left( { - 2} \right) - 1}}{{ - 2 - 1}} = - 1.\)
Chọn A.







