Phương pháp giải:

+ Điều kiện để có sóng dừng trên dây hai đầu cố định là : 

\(l = k\frac{\lambda }{2}\)

Trong đó: Số bụng = k; Số nút = k + 1.

+ Các điểm trong cùng một bó sóng thì dao động cùng pha, các điểm thuộc hai bó sóng liên tiếp thì dao động ngược pha.

Sử dụng hình vẽ.

Lời giải chi tiết:

Điều kiện để có sóng dừng trên dây hai đầu cố định là:

\(l = k\frac{\lambda }{2} = 2,5\lambda \Rightarrow k = 5\)

Vậy trên dây AB có 5 bụng.

Phương trình dao động của điểm M cách A một khoảng d là:

\({u_M} = 2a.\sin \left( {\frac{{2\pi d}}{\lambda }} \right).\cos \left( {\omega t + \varphi - \frac{{2\pi l}}{\lambda } - \frac{\pi }{2}} \right)\)

M cách A một khoảng 1,8λ nên ta có vị trí của M:

\({x_M} = 3,6\frac{\lambda }{2}\) nên M nằm trong bó sóng thứ 4 kể từ A.

Ta có hình vẽ:

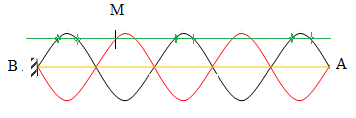
Các điểm cùng biên độ với M và ngược pha được đánh dấu, vậy có 6 điểm.

Chọn B.