Câu hỏi
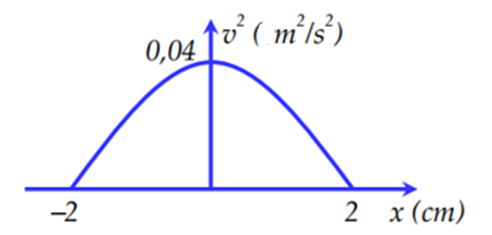
Một vật dao động điều hòa dọc theo trục Ox, có đồ thị biểu diễn sự phụ thuộc của bình phương vận tốc (v2) vào li độ x như hình vẽ. Tần số góc của vật là
- A 10 rad/s.
- B 2 rad/s.
- C 20 rad/s.
- D 40 rad/s
Phương pháp giải:
Phương trình của li độ và vận tốc:
\(\left\{ \begin{array}{l}
x = A.\cos \left( {\omega t + \varphi } \right)\\
v = - \omega A.\sin \left( {\omega t + \varphi } \right)
\end{array} \right.\)
Lời giải chi tiết:
Phương trình dao động điều hòa và phương trình vận tốc:
\(\begin{array}{l}
\left\{ \begin{array}{l}
x = A.\cos \left( {\omega t + \varphi } \right)\\
v = - \omega A.\sin \left( {\omega t + \varphi } \right) \Rightarrow {v^2} = {\omega ^2}.{A^2}.{\sin ^2}\left( {\omega t + \varphi } \right)
\end{array} \right.\\
\Rightarrow {v^2} = {\omega ^2}.\left( {{A^2} - {x^2}} \right)
\end{array}\)
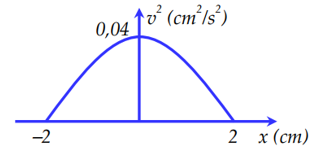
Từ đồ thị, ta thấy biên độ A = 2cm và tại \({x = 0;{v^2} = 0,04}\)
Vậy ta có :
\({v^2} = {\omega ^2}.{A^2} = 0,04 \Rightarrow \omega = \sqrt {\frac{{{v^2}}}{{{A^2}}}} = \sqrt {\frac{{0,04}}{{0,{{02}^2}}}} = 10\left( {rad/s} \right)\)
Chọn A.







