Câu hỏi
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, \(AB = 2a,\)\(AD = a\)\(\left( {a > 0} \right)\). M là trung điểm của AB, tam giác SMC vuông tại S, \(\left( {SMC} \right) \bot \left( {ABCD} \right),\)\(SM\) tạo với đáy góc \(60^\circ \). Thể tích của khối chóp S.ABCD là:
- A \(\dfrac{{{a^3}\sqrt 6 }}{6}.\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{6}.\)
- C \(\dfrac{{2{a^3}\sqrt 6 }}{3}.\)
- D \(\dfrac{{{a^3}}}{3}.\)
Phương pháp giải:
- Trong \(\left( {SMC} \right)\) kẻ \(SI \bot MC\,\,\left( {I \in MC} \right)\), chứng minh \(SI \bot \left( {ABCD} \right)\).
- Xác định góc giữa \(SM\) và mặt đáy là góc giữa \(SM\) và hình chiếu của \(SM\) lên mặt đáy.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao \(SI\).
- Tính thể tích khối chóp \({V_{S.ABCD}} = \dfrac{1}{3}SI.{S_{ABCD}}\).
Lời giải chi tiết:
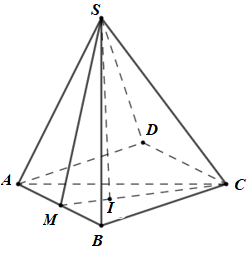
Trong \(\left( {SMC} \right)\) kẻ \(SI \bot MC\,\,\left( {I \in MC} \right)\) ta có: \(\left\{ \begin{array}{l}\left( {SMC} \right) \bot \left( {ABCD} \right) = MC\\SI \subset \left( {SMC} \right),\,\,SI \bot MC\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
\( \Rightarrow IM\) là hình chiếu của \(SM\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SM;\left( {ABCD} \right)} \right) = \angle \left( {SM;IM} \right) = \angle SMI = \angle SMC = {60^0}\).
Áp dụng định lí Pytago trong tam giác BMC vuông tại B :
\(BM = \dfrac{{AB}}{2} = a;\,\,BC = a\)\( \Rightarrow MC = \sqrt {B{C^2} + B{M^2}} = a\sqrt 2 \).
Xét tam giác SMC vuông tại \(S\) có \(\angle SMC = {60^0};\,\,MC = a\sqrt 2 \) \( \Rightarrow SM = MC.\cos {60^0} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác SMI vuông tại \(I\) có \(\angle SMI = {60^0};\,\,SM = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow SI = SM.sin{60^0} = \dfrac{{a\sqrt 2 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{4}\).
Vậy thể tích khối chóp là \(V = \dfrac{1}{3}SI.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.2{a^2} = \dfrac{{{a^3}\sqrt 6 }}{6}.\)
Chọn A.







