Phương pháp giải:

Diện tích của đường tròn bán kính \(r\) là: \(S = \pi {r^2}.\)

Thể tích khối nón có chiều cao \(h\) và bán kính đáy \(R\) là: \(V = \dfrac{1}{3}\pi {R^2}h.\)

Lời giải chi tiết:

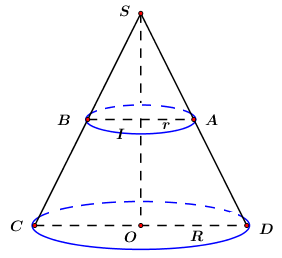
Mặt phẳng vuông góc và đi qua trung điểm \(I\)  của trục \(SO\) của  khối nón cắt khối nón tròn xoay theo giao tuyến là đường tròn tâm \(I\) bán kính \(r.\)

\( \Rightarrow \pi {r^2} = 9\pi  \Leftrightarrow r = 3.\)

Theo định lý Ta-let ta có: \(\dfrac{{SI}}{{SO}} = \dfrac{r}{R} = \dfrac{1}{2}\) \( \Leftrightarrow R = 2r = 6.\)

\( \Rightarrow \) Thể tích khối nón đã cho là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.6^2}.6 = 72\pi .\)

Chọn C.