Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

Để q₃ cân bằng thì \(\overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  + \overrightarrow {{F_{03}}}  = 0\,\,\left( * \right)\)

Đặt \(\overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}} \)

Có: \(\left\{ \begin{array}{l}{q_1} = {q_2}\\AC = BC = a\end{array} \right. \Rightarrow {F_{13}} = {F_{23}} \Rightarrow F = 2{F_{13}}.cos30 = {F_{13}}.\sqrt 3 \)

\(\left( * \right) \Leftrightarrow \overrightarrow F  + \overrightarrow {{F_{03}}}  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow F  \uparrow  \downarrow \overrightarrow {{F_{03}}} \,\,\,\left( 1 \right)\\F = {F_{03}}\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Từ (1) \( \Rightarrow \overrightarrow {{F_{03}}} \) nằm trên đường phân giác của góc \(\widehat {ACB}\) và \({q_0} < 0\)

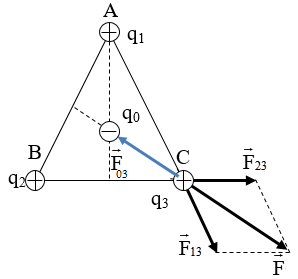
Làm tương tự với \({q_1};{q_2} \Rightarrow {q_0}\) nằm tại trọng tâm của \(\Delta ABC\) và \({q_0} < 0\)

Từ (2)\( \Rightarrow F = {F_{03}} \Leftrightarrow {F_{13}}\sqrt 3  = {F_{03}} \Leftrightarrow \sqrt 3 .\dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{{a^2}}} = \dfrac{{k.\left| {{q_0}{q_3}} \right|}}{{{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}}\)

\( \Leftrightarrow \sqrt 3 .\left| {{q_1}} \right| = 3.\left| {{q_0}} \right| \Rightarrow \left| {{q_0}} \right| = \dfrac{{2\sqrt 3 {{.10}^{ - 6}}}}{{\sqrt 3 }} = {2.10^{ - 6}}C\)

Vậy \({q_0} =  - {2.10^{ - 6}}C\)

Kiểm tra với q₀ thì thấy q₀ cũng cân bằng.

Vậy \({q_0}\) nằm ở trọng tâm của ∆ABC; \({q_0} =  - {2.10^{ - 6}}C\)

Chọn A.