Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên (SAD) là tam giác vuông tại S. Hình chiếu vuông góc của S trên mặt đáy là điểm H thuộc AD sao cho HA = 3HD. Biết \(SA = 2a\sqrt 3 \), SC tạo với đáy một góc \({30^0}\). Gọi M là trung điểm AB. Tính \({d_{\left[ {M;\left( {SBC} \right)} \right]}}\).
- A \(2a\sqrt 3 \)
- B \(\dfrac{{a\sqrt 3 }}{4}\)
- C \(\dfrac{{a\sqrt 3 }}{2}\)
- D \(a\sqrt 3 \)
Phương pháp giải:
- Đổi \(d\left( {M;\left( {SBC} \right)} \right) = d\left( {H;\left( {SBC} \right)} \right)\).
- Xác định khoảng cách.
- Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\) là góc giữa \(SC\) và hình chiếu của \(SC\) lên \(\left( {ABCD} \right)\).
- Đặt \(SH = x\). Tính \(HC,\,\,SC,\,\,AB,\,\,BH,\,\,SB,\,\,BC\) theo \(x\).
- Áp dụng định lí Pytago trong tam giác vuông \(SBC\) thiết lập phương trình giữa \(x,\,\,a\). Giải phương trình tìm \(x\) theo \(a\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
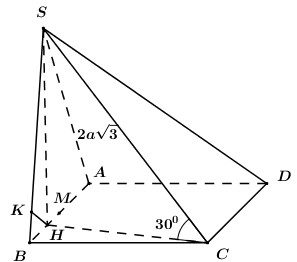
Ta có \(MH \cap \left( {SBC} \right) = B \Rightarrow \dfrac{{d\left( {M;\left( {SBC} \right)} \right)}}{{d\left( {H;\left( {SBC} \right)} \right)}} = \dfrac{{MB}}{{HB}}\).
Ta có \(\dfrac{{MB}}{{HB}} = \dfrac{{AB}}{2}:\dfrac{{AB}}{4} = 2\) \( \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = 2d\left( {H;\left( {SBC} \right)} \right)\).
Trong \(\left( {SAB} \right)\) dựng \(HK \bot SB\,\,\left( {K \in SB} \right)\) ta có:
+ \(\left\{ \begin{array}{l}BC \bot SH\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot HK\).
+ \(\left\{ \begin{array}{l}HK \bot SB\\HK \bot BC\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right)\) \( \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HK\).
+ Đặt \(SH = x\).
+ \(\angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {30^0}\).
+ \(\Delta SHC:\,\,HC = SH.cot{30^0} = x\sqrt 3 \), \(SC = \dfrac{{SH}}{{\sin {{30}^0}}} = 2x\).
+ \(\Delta SAH\): \(AH = \sqrt {S{A^2} - S{H^2}} = \sqrt {12{a^2} - {x^2}} \)
\( \Rightarrow AB = \dfrac{4}{3}AH = \dfrac{4}{3}\sqrt {12{a^2} - {x^2}} \), \(BH = \dfrac{1}{4}AB = \dfrac{1}{3}\sqrt {12{a^2} - {x^2}} \).
+ \(\Delta SAB:\,\,SB = \dfrac{{SH.AB}}{{SA}} = \dfrac{{x.\dfrac{4}{3}\sqrt {12{a^2} - {x^2}} }}{{2a\sqrt 3 }} = \dfrac{{2x\sqrt {12{a^2} - {x^2}} }}{{3a\sqrt 3 }}\).
+ \(\Delta BCH:\,\,BC = \sqrt {C{H^2} - B{H^2}} = \sqrt {3{x^2} - \dfrac{{12{a^2} - {x^2}}}{9}} = \dfrac{{2\sqrt {7{x^2} - 3{a^2}} }}{3}\).
+ \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại \(B\).
\(\begin{array}{l} \Rightarrow S{B^2} + B{C^2} = S{C^2}\\ \Leftrightarrow {\left( {\dfrac{{2x\sqrt {12{a^2} - {x^2}} }}{{3a\sqrt 3 }}} \right)^2} + {\left( {\dfrac{{2\sqrt {7{x^2} - 3{a^2}} }}{3}} \right)^2} = 4{x^2}\\ \Leftrightarrow \dfrac{{4{x^2}\left( {12{a^2} - {x^2}} \right)}}{{27{a^2}}} + \dfrac{{4\left( {7{x^2} - 3{a^2}} \right)}}{9} = 4{x^2}\\ \Leftrightarrow \dfrac{{48{a^2}{x^2} - 4{x^4} + 84{x^2}{a^2} - 36{a^4}}}{{27{a^2}}} = 4{x^2}\\ \Leftrightarrow 132{a^2}{x^2} - 4{x^4} - 36{a^4} = 108{a^2}{x^2}\\ \Leftrightarrow 4{x^4} + 36{a^4} - 24{a^2}{x^2} = 0\\ \Leftrightarrow {\left( {2{x^2} - 6{a^2}} \right)^2} = 0\\ \Leftrightarrow 2{x^2} = 6{a^2}\\ \Leftrightarrow {x^2} = 3{a^2} \Leftrightarrow x = a\sqrt 3 = SH\\ \Rightarrow BH = \dfrac{1}{3}\sqrt {12{a^2} - {x^2}} = a\end{array}\)
+ \(\Delta SHB:\,\,HK = \dfrac{{SH.BH}}{{\sqrt {S{H^2} + B{H^2}} }} = \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}\).
Vậy \(d\left( {M;\left( {SBC} \right)} \right) = a\sqrt 3 \).







