Câu hỏi
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k gắn với vật nhỏ có khối lượng m đang dao động điều hòa. Lực đàn hồi lò xo tác dụng lên vật trong quá trình dao động có đồ thị như hình vẽ. Thời gian lò xo bị nén trong một chu kì là
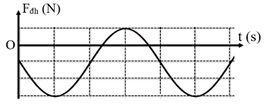
- A \(\dfrac{{2\pi }}{3}\sqrt {\dfrac{m}{k}} \).
- B \(\dfrac{\pi }{6}\sqrt {\dfrac{m}{k}} \).
- C \(\dfrac{\pi }{3}\sqrt {\dfrac{m}{k}} \).
- D \(\dfrac{{4\pi }}{3}\sqrt {\dfrac{m}{k}} \).
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thị
Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\)
Lời giải chi tiết:
Ta có trục đối xứng của đồ thị:
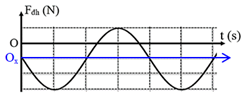
Vị trí O là vị trí lò xo không bị biến dạng
Từ đồ thị ta thấy: \({O_x}O = \Delta {\rm{l = }}\frac{A}{2}\)
Ta có vòng tròn lượng giác:
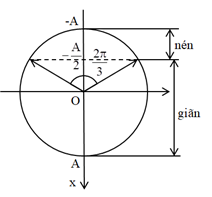
Từ vòng tròn lượng giác, ta thấy trong khoảng thời gian lò xo nén trong 1 chu kì, vecto quay được góc:
\(\Delta \varphi = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right) \Rightarrow \Delta {t_{nen}} = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{2\pi }}{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{3} = \dfrac{1}{3}.2\pi \sqrt {\dfrac{m}{k}} = \dfrac{{2\pi }}{3}\sqrt {\dfrac{m}{k}} \)
Chọn A.







