Câu hỏi
Trong không gian, cho hình chữ nhật ABCD, \(AB = a\), \(AC = 2a\). Khi quay hình chữ nhật ABCD quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung quanh của hình trụ đó bằng:
- A \(\dfrac{{\pi {a^2}}}{{\sqrt 3 }}.\)
- B \(\dfrac{{2\pi {a^2}}}{{\sqrt 3 }}.\)
- C \(4\pi {a^2}.\)
- D \(2\sqrt 3 \pi {a^2}.\)
Phương pháp giải:
- Xác định đáy, chiều cao của hình trụ.
- Áp dụng công thức tính diện tích xung quanh hình trụ: \(S = 2\pi rh\).
Lời giải chi tiết:
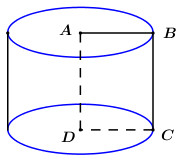
Quay hình chữ nhật ABCD quanh cạnh AD ta được hình trụ có bán kính là \(r = AB = a\) và chiều cao là \(h = BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \).
Vây diện tích xung quanh hình trụ:\(S = 2\pi rh = 2\pi a.a\sqrt 3 = 2\sqrt 3 \pi {a^2}.\)
Chọn D.
Câu hỏi trước
