Câu hỏi
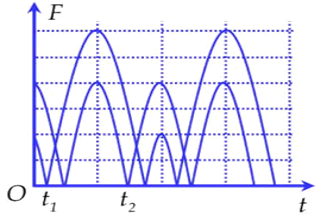
Một con lắc được treo vào một điểm cố định, đang dao động điều hòa theo phương thẳng đứng. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của độ lớn của lực kéo về và độ lớn của lực đàn hồi của lò xo tác dụng lên vật theo thời gian. Lấy g = 10 m/s2. Biết \({t_2} - {t_1} = \frac{{7\pi }}{{120}}s\). Tốc độ cực đại của con lắc gần nhất với giá trị nào sau đây?
- A 78 cm/s
- B 98 cm/s.
- C 85 cm/s.
- D 105 cm/s.
Phương pháp giải:
Biểu thức lực hồi phục: \(F = - kx\)
Biểu thức lực đàn hồi: \(F = - k\left( {x + \Delta {l_0}} \right)\)
Từ đồ thị dễ thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục.
Đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi.
Lập tỉ số tại các cực trị, ta tìm được ∆l0 theo A
Thời điểm t1 ứng với vị trí lò xo không dãn.
Thời điểm t2 ứng với vị trí cân bằng.
Sử dụng ĐTLG từ thời điểm t1 đến t2 tìm được chu kì T, ∆l0 và A.
Tốc độ cực đại:
\({v_{\max }} = \omega A = A.\sqrt {\frac{g}{{\Delta l}}} \)
Lời giải chi tiết:
Biểu thức lực hồi phục và lực đàn hồi:
\(\left\{ \begin{array}{l}
{F_{hp}} = - kx\\
{F_{dh}} = - k\left( {x + \Delta {l_0}} \right)
\end{array} \right.\)
Từ đồ thị dễ thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục.
Đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi.
Lập tỉ số tại các cực trị:
\(\frac{{{F_{dh\max }}}}{{{F_{hp\max }}}} = \frac{{k.(A + \Delta {l_0})}}{{kA}} = \frac{6}{4} \Rightarrow \Delta {l_0} = \frac{A}{2}\)
Thời điểm t1 ứng với vị trí lò xo không dãn.
Thời điểm t2 ứng với vị trí cân bằng.
Sử dụng ĐTLG từ thời điểm t1 đến t2
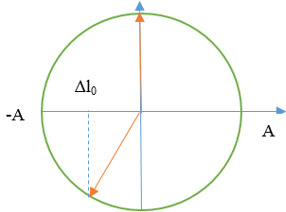
Thời gian từ t1 đến t2 là :
\(\begin{array}{l}
\Delta t = {t_2} - {t_1} = \left( {\arcsin \frac{{\Delta {l_0}}}{A} + \frac{\pi }{2}} \right).\frac{T}{{2\pi }} = \frac{{7T}}{{12}} = \frac{{7\pi }}{{120}}\\
\Rightarrow T = \frac{\pi }{{10}}s \Rightarrow \omega = \frac{{2\pi }}{T} = 20rad/s
\end{array}\)
Với
\(\omega = \sqrt {\frac{g}{{\Delta {l_0}}}} \Rightarrow 20 = \sqrt {\frac{{10}}{{\Delta {l_0}}}} \Rightarrow \Delta {l_0} = 0,025m = 2,5cm \Rightarrow A = 5cm\)
Tốc độ cực đại:
\(v = \omega A = 20.5 = 100\left( {cm/s} \right)\)
Gần nhất với giá trị 98 cm/s
Chọn B.







