Câu hỏi
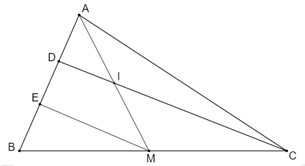
Cho tam giác ABC có trung tuyến AM, trên đoạn AB lấy 2 điểm D và E sao cho\(AD = DE = EB\). Gọi I là giao điểm CD và AM. Chứng minh I là trung điểm AM.
Phương pháp giải:
Áp dụng định lý 1 đường trung bình của tam giác: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Xét \(\Delta BDC\) ta có: \(M,\,\,E\) lần lượt là trung điểm các cạnh \(BC,\,\,BD\)
\( \Rightarrow ME\) là đường trung bình của \(\Delta BDC.\) (định nghĩa)
\( \Rightarrow ME//CD.\)
Xét \(\Delta AEM\) ta có: \(D\) là trung điểm của \(AE\)
\(DE//ME\,\,\,\left( {DC//ME} \right)\)
\( \Rightarrow I\) là trung điểm của \(AM.\) (định lý đảo)